题目内容

4．已知向量$\overrightarrow{a}$=（4，2），$\overrightarrow{b}$=（x，3），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则x的值是（　　）
A．-6B．6C．-$\frac{3}{2}$D．$\frac{3}{2}$

分析 根据平面向量的坐标表示与共线定理，列出方程求出x的值．

解答 解：∵向量$\overrightarrow{a}$=（4，2），$\overrightarrow{b}$=（x，3），且$\overrightarrow{a}$∥$\overrightarrow{b}$，
∴2x-3×4=0，
解得x=6．
故选：B．

点评 本题考查了平面向量的坐标表示与共线定理的应用问题，是基础题目．

练习册系列答案
相关题目
14．已知函数$f（x）=2sinxcosx+2\sqrt{3}{cos^2}x-\sqrt{3}$．
（1）求函数f（x）的最小正周期和单调减区间；
（2）已知△ABC的三个内角A，B，C的对边分别为a，b，c，其中a=7，若锐角A满足$f（\frac{A}{2}-\frac{π}{6}）=\sqrt{3}$，且$sinB+sinC=\frac{{13\sqrt{3}}}{14}$，求△ABC的面积．
15．已知等比数列{an}、等差数列{bn}，满足a1＞0，b1=a1-1，b2=a2，b3=a3．
（1）若a1=$\frac{1}{4}$，求数列{an}，{bn}的通项公式；
（2）若数列{an}唯一，求数列{an•bn}、的前n项和．
12．设x∈R，则“1-x-2x2＜0”是“|2-x|＜1”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
19．执行如图所示的程序框图，则输出i的值为（　　）
A．4B．5C．6D．55
9．已知复数z满足（1+i）z=（1-i）2，则z的共轭复数的虚部为（　　）
A．2B．-2C．-1D．1
16．已知直线l1：A1x+B1y+1=0，直线l2：A2x+B2y+1=0，A1，A2，B1，B2∈R，则“l1⊥l2”的充分且必要条件是（　　）
A．A1A2-B1B2=0B．A1A2+B1B2=0C．A1B2-A2B1=0D．A1B2+A2B1=0
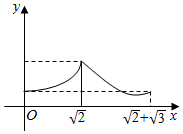
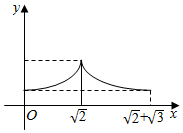
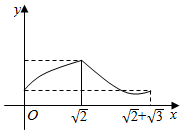
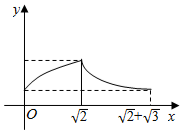
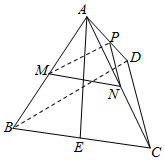13．已知圆C：（x-1）2+（y-2）2=2，若等边△PAB的一边AB为圆C的一条弦，则|PC|的最大值为2$\sqrt{2}$．
14．如图，在正三棱锥A-BCD中，M，N，E分别为AB，AC，BC边的中点，侧棱长为$\sqrt{2}$，且三条棱两两垂直，点P由A向E沿A→D→E运动，设点P运动的路程为x，△PMN的面积为y，则函数y=f（x）的图象大致是（　　）
A．B．
C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网