题目内容
奇函数f(x)满足f(x)=f(a-x)的周期为 .
考点:函数的周期性
专题:函数的性质及应用
分析:令x取x+a代入f(x)=f(a-x)得f(x+a)=f(-x),利用奇函数的性质可得f(x+a)=-f(x),令x取x+a代入化简后,由周期函数的定义即可求出函数f(x)的周期.
解答:
解:令x取x+a代入f(x)=f(a-x)得,f(x+a)=f(-x),
因为f(x)是奇函数,所以f(-x)=-f(x),
则f(x+a)=-f(x),令x取x+a代入得,
f(x+2a)=-f(x+a)=f(x),
所以函数f(x)的周期是2a,
故答案为:2a.
因为f(x)是奇函数,所以f(-x)=-f(x),
则f(x+a)=-f(x),令x取x+a代入得,
f(x+2a)=-f(x+a)=f(x),
所以函数f(x)的周期是2a,
故答案为:2a.
点评:本题考查奇函数的性质,以及周期函数的定义的应用,属于基础题.

练习册系列答案
相关题目
已知抛物线y2=2px(p>0)的焦点为F,抛物线上的3个点A,B,C的横坐标之比为3:4:5,则以|FA|,|FB|,|FC|为边长的三角形( )
| A、不存在 |
| B、必是锐角三角形 |
| C、必是钝角三角形 |
| D、必是直角三角形 |
方程
•
=|x+y-2|表示的曲线是( )
| 2 |
| (x+1)2+(y+1)2 |
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、不能确定 |
在△ABC中,三个内角A,B,C的对边分别为a,b,c,若
=
,则∠B的值为( )
| a |
| sinA |
| b |
| cosB |
| A、30° | B、45° |
| C、60° | D、90° |
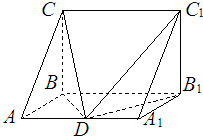 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=