题目内容
已知点M是y=
x2上一点,F为抛物线的焦点,A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为 .
| 1 |
| 4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:首先求出抛物线上的点到圆上及抛物线的焦点的距离最小的位置,然后根据三点共线求出相应的点的坐标,进一步求出最小值.
解答:
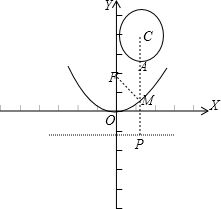
解:如上图所示
利用抛物线的定义知:MP=MF
当M、A、P三点共线时,|MA|+|MF|的值最小
即:CM⊥x轴
CM所在的直线方程为:x=1与y=
x2建立方程组解得:M(1,
)
|CM|=4-
点M到圆C的最小距离为:|CM|-|AC|=3
抛物线的准线方程:y=-1
则:,|MA|+|MF|的值最小值为3+1=4
故答案为:4

解:如上图所示
利用抛物线的定义知:MP=MF
当M、A、P三点共线时,|MA|+|MF|的值最小
即:CM⊥x轴
CM所在的直线方程为:x=1与y=
| 1 |
| 4 |
| 1 |
| 4 |
|CM|=4-
| 1 |
| 4 |
点M到圆C的最小距离为:|CM|-|AC|=3
抛物线的准线方程:y=-1
则:,|MA|+|MF|的值最小值为3+1=4
故答案为:4
点评:本题考查的知识点:圆外一点到圆的最小距离,抛物线的准线方程,三点共线及相关的运算问题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
 如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.
如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: