题目内容
如果函数y=logax在区间[2,+∞﹚上恒有y>1,求实数a的取值范围.
考点:对数函数的单调区间
专题:函数的性质及应用
分析:根据函数y=logax在区间[2,+∞﹚上恒有y>1,
必须单调递增,
所以转化loga
>1解不等式即可求出a的范围.
必须单调递增,
所以转化loga
2 |
解答:
解:∵函数y=logax在区间[2,+∞﹚上恒有y>1,∴loga2>1,
当a>1时,lo
>log
,
即1<a<2,
当0<a<1时,lo
>log
,无解.
综上实数a的取值范围:(1,2)
当a>1时,lo
2 a |
a a |
即1<a<2,
当0<a<1时,lo
2 a |
a a |
综上实数a的取值范围:(1,2)
点评:本题综合考查了对数函数的单调性,对数的运算,注意分类讨论求解.

练习册系列答案
相关题目
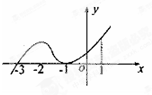 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3是函数y=f(x)的极小值点;
②-1是函数y=f(x)的极值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
 如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.
如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.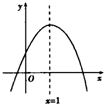 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: