题目内容
在实数集R中定义一种运算“*”,?a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
关于函数f(x)=(ex)•
的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
其中所有正确说法的个数为( )
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
关于函数f(x)=(ex)•
| 1 |
| ex |
其中所有正确说法的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:阅读型,新定义,函数的性质及应用
分析:性质(2)可由性质(1)化简得,a*b=ab+a+b.则f(x)=1+ex+
,由基本不等式,即可判断①;
由奇偶性的定义,求出f(-x),即可判断②;可求出f(x)的导数,令导数不小于0,解出即可判断③.
| 1 |
| ex |
由奇偶性的定义,求出f(-x),即可判断②;可求出f(x)的导数,令导数不小于0,解出即可判断③.
解答:
解:由于对任意a,b∈R,a*b=ab+(a*0)+(b*0),
则由对任意a∈R,a*0=a,可得a*b=ab+a+b.
则有f(x)=(ex)•
=ex•
+ex+
=1+ex+
对于①,由于定义域为R,则ex>0,1+ex+
≥1+2
=3,
当且仅当ex=
,即有x=0,f(x)取最小值3,故①对;
对于②,由于定义域为R,关于原点对称,且f(-x)=1+e-x+
=1+ex+
=f(x),
则f(x)为偶函数,故②对;
对于③,f′(x)=ex-e-x,令f′(x)≥0,则x≥0,即f(x)的单调递增区间为[0,+∞),故③错.
故选:C.
则由对任意a∈R,a*0=a,可得a*b=ab+a+b.
则有f(x)=(ex)•
| 1 |
| ex |
| 1 |
| ex |
| 1 |
| ex |
=1+ex+
| 1 |
| ex |
对于①,由于定义域为R,则ex>0,1+ex+
| 1 |
| ex |
ex•
|
当且仅当ex=
| 1 |
| ex |
对于②,由于定义域为R,关于原点对称,且f(-x)=1+e-x+
| 1 |
| e-x |
| 1 |
| ex |
则f(x)为偶函数,故②对;
对于③,f′(x)=ex-e-x,令f′(x)≥0,则x≥0,即f(x)的单调递增区间为[0,+∞),故③错.
故选:C.
点评:本题是一个新定义运算型问题,考查了函数的最值、奇偶性、单调性等有关性质以及同学们类比运算解决问题的能力.

练习册系列答案
相关题目
已知{an}是等比数列,对任意n∈N*都有an>0,如果a3(a3+a5)+a4(a4+a6)=25,则a3+a5=( )
| A、5 | B、10 | C、15 | D、20 |
 如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.
如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.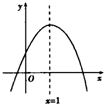 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: