题目内容
17．函数y=2sin（ωx+φ）是偶函数，则φ可能等于（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | π |
分析 根据函数的对称性得出φ．
解答 解：∵y=2sin（ωx+φ）是偶函数，
∴x=0是y=2sin（ωx+φ）的对称轴．
∴sinφ=±1．
∴φ=$\frac{π}{2}+kπ$．k∈Z．
故选C．
点评 本题考查了正弦函数的图象与性质，属于基础题．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
12．己知x，y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取到最小值2$\sqrt{5}$时，则4a2+b2的最小值为（ ）
| A． | 5 | B． | 10 | C． | $\sqrt{5}$ | D． | $\sqrt{10}$ |
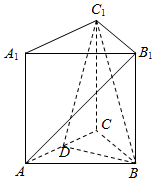如图，在三棱柱ABC-A1B1C1中，C1C⊥底面ABC，CC1=AB=AC=BC=4，D为线段AC的中点．
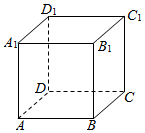如图，正方体ABCD-A1B1C1D1的棱长为1，请在此正方体中取出四个顶点构成一个三棱锥，满足三棱锥的四个面都是直角三角形，并求此三棱锥的体积．
6．将函数f（x）=sin（2x-$\frac{π}{3}$）的图象向左平移φ（φ＞0）个单位，所得图象对应的函数为奇函数，则φ的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |