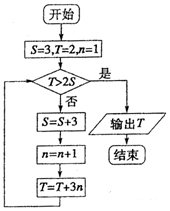
题目内容
14.P为抛物线x2=-4y上一点,A(2$\sqrt{2}$,0),则P到此抛物线的准线的距离与P到点A的距离之和的最小值为3.分析 利用抛物线的定义结合不等式求解即可.
解答 解:因为P为抛物线x2=-4y上一点,A(2$\sqrt{2}$,0)在抛物线的外侧,由抛物线的定义可得:P到准线的距离d等于到焦点的距离,则P到此抛物线的准线的距离与P到点A的距离之和为:d+|PA|=|PF|+|PA|≥|AF|=3,
所求的最小值为3.
故答案为:3.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
5.某汽车的使用年数x与所支出的维修费用y的统计数据如表:
根据上表可得y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x-0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
| 使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
| 维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
| A. | 8年 | B. | 9年 | C. | 10年 | D. | 11年 |
2.已知直线ax-y+2a=0的倾斜角为$\frac{3π}{4}$,则a等于( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
9.复数z=(1-i)(4-i)的共轭复数的虚部为( )
| A. | -5i | B. | 5i | C. | -5 | D. | 5 |
6.三位老师和三位学生站成一排,要求任何两位学生都不相邻,则不同的排法总数为( )
| A. | 720 | B. | 144 | C. | 36 | D. | 12 |
4.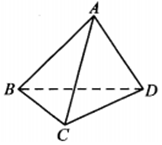 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )| A. | θ的最大值为60° | B. | θ的最小值为60° | C. | θ的最大值为30° | D. | θ的最小值为30° |