题目内容
11．已知A（0，1）和直线l：x=-5，抛物线y2=4x上动点P到l的距离为d，则|PA|+d的最小值是（ ）| A． | 6 | B． | $5+\sqrt{2}$ | C． | $4+\sqrt{2}$ | D． | $4\sqrt{2}$ |
分析 先求出抛物线的准线方程为直线x=-1，再根据抛物线的基本性质可得当焦点、P点、A点共线时距离最小，从而得到答案．
解答 解：抛物线准线为x=-1，P到其距离为d1，则d=d1+4，
所以$|{PA}|+d=4+{d_1}+|{PA}|=4+|{PF}|+|{PA}|≥4+|{FA}|=4+\sqrt{2}$．
故选C．
点评 考查圆锥曲线的定义及数形结合，化归转化的思想方法．
练习册系列答案
相关题目
2．某几何体的三视图如图所示，其则该几何体的体积是（ ）
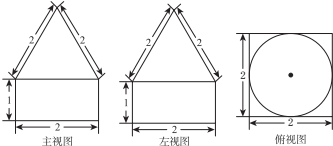
| A． | $2+\frac{{\sqrt{3}}}{3}π$ | B． | $4+\sqrt{3}π$ | C． | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D． | $4+\frac{{\sqrt{3}}}{3}π$ |
某单位拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x米，圆心角为θ（弧度）．