题目内容
若实数a,b满足a2+b2=1,则a
的最大值是 ,此时a= ,b= .
| 1+b2 |
考点:基本不等式在最值问题中的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:首先可知当a
取得最大值时,a>0;从而化简a
=
,从而利用利用不等式求最值.
| 1+b2 |
| 1+b2 |
| a2(1+b2) |
解答:
解:当a
取得最大值时,a>0;
a
=
≤
=1;
(当且仅当a=1,b=0时,等号成立)
故a
的最大值是1,
此时,a=1,b=0;
故答案为:1,1,0.
| 1+b2 |
a
| 1+b2 |
| a2(1+b2) |
| a2+1+b2 |
| 2 |
(当且仅当a=1,b=0时,等号成立)
故a
| 1+b2 |
此时,a=1,b=0;
故答案为:1,1,0.
点评:本题考查了基本不等式在求最值问题中的应用,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
用二分法求方程近似解的过程中,已知在区间[a,b]上,f(a)>0,f(b)<0,并计算得到f(
)<0,那么下一步要计算的函数值为( )
| a+b |
| 2 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|
设f(x)=|x-a|是偶函数,g(x)=2x+
是奇函数,那么a+b的值为( )
| b |
| 2x |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
若P(x,y)在圆(x+3)2+(y-3)2=6上运动,则
的最大值等于( )
| y |
| x |
A、-3+2
| ||
B、-3+
| ||
C、-3-2
| ||
D、3-2
|
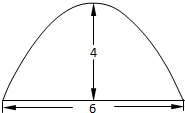 如图,一个抛物线型拱桥,当水面离拱顶4m时,水面的宽6m.经过一段时间的降雨后,水面上升了1m,此时水面宽度为
如图,一个抛物线型拱桥,当水面离拱顶4m时,水面的宽6m.经过一段时间的降雨后,水面上升了1m,此时水面宽度为