题目内容
已知函数f(x)=log4(4x+1)+kx(x∈R)的图象关于y轴对称.
(1)求k的值;
(2)若函数y=f(x)的图象与直线y=
x+b没有交点,求实数b的取值范围.
(3)设g(x)=log4(a•2x-a•m),当m取任意正数时,是否存在实数a,使得函数f(x)与 g(x)的图象有且只有一个公共点?若存在,求实数a的取值范围;若不存在,请说明理由.
(1)求k的值;
(2)若函数y=f(x)的图象与直线y=
| 1 |
| 2 |
(3)设g(x)=log4(a•2x-a•m),当m取任意正数时,是否存在实数a,使得函数f(x)与 g(x)的图象有且只有一个公共点?若存在,求实数a的取值范围;若不存在,请说明理由.
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:(1)根据偶函数可知f(x)=f(-x),取x=-1代入即可求出k的值;
(2)由(1)中结论,可以得到函数的解析式,构造函数y=log4(4x+1)-x,分析出函数的单调性及值域,根据函数零点的判定方法,我们易确定b取不同值时,函数零点个数,进而得到答案.
(3)函数f(x)与g(x)的图象有且只有一个公共点,则方程f(x)=g(x)有且只有一个实根,化简可得 2x+
=a•2x-a•m,有且只有一个实根,令t=2x>0,则转化才方程 (a-1)t2-amt-1=0,有且只有一个正根,讨论a=1,以及△=0与一个正根和一个负根,三种情形,即可求出实数a的取值范围.
(2)由(1)中结论,可以得到函数的解析式,构造函数y=log4(4x+1)-x,分析出函数的单调性及值域,根据函数零点的判定方法,我们易确定b取不同值时,函数零点个数,进而得到答案.
(3)函数f(x)与g(x)的图象有且只有一个公共点,则方程f(x)=g(x)有且只有一个实根,化简可得 2x+
| 1 |
| 2x |
解答:
解:(1)∵f(x)=log4(4x+1)+kx(k∈R)的图象关于y轴对称.
∴函数f(x)是偶函数.
∴f(-x)=f(x)
即log4(4-x+1)-kx=log4(4x+1)+kx
即log4(4x+1)-(k+1)x=log4(4x+1)+kx
即2k+1=0
∴k=-
;
证明:(2)由(1)得f(x)=log4(4x+1)-
x,
令y=log4(4x+1)-x-b
由于y=log4(4x+1)-x-b为减函数,且恒为正,
故当b>0时,y=log4(4x+1)-x-b有唯一的零点,此时函数y=f(x)的图象与直线y=
x+b有一个交点,
当b≤0时,y=log4(4x+1)-x-b没有零点,此时函数y=f(x)的图象与直线y=
x+b没有交点,
综上所述,b≤0时,函数y=f(x)的图象与直线y=
x+b没有交点;
(3)∵g(x)=log4(a•2x-a•m),∴a≠0,
函数f(x)与g(x)的图象有且只有一个公共点
即方程 log4(4x+1)-
x=log4(a•2x-a•m),有且只有一个实根,
化简得:方程 2x+
=a•2x-a•m有且只有一个实根,
令t=2x>0,m=
,则方程 t+
=at-am,即(a-1)t2-
at-1=0,有且只有一个正根,
①当a=1时,t=-
<0,不合题意;
②当a≠1时,△=0⇒a=
或-3,
若a=
,则t=-
,不合题意;若a=-3,则t=
成立,
③若一个正根和一个负根,则
<0,即a>1时,满足题意.
所以实数a的取值范围为{a|a>1或a=-3}.
∴函数f(x)是偶函数.
∴f(-x)=f(x)
即log4(4-x+1)-kx=log4(4x+1)+kx
即log4(4x+1)-(k+1)x=log4(4x+1)+kx
即2k+1=0
∴k=-
| 1 |
| 2 |
证明:(2)由(1)得f(x)=log4(4x+1)-
| 1 |
| 2 |
令y=log4(4x+1)-x-b
由于y=log4(4x+1)-x-b为减函数,且恒为正,
故当b>0时,y=log4(4x+1)-x-b有唯一的零点,此时函数y=f(x)的图象与直线y=
| 1 |
| 2 |
当b≤0时,y=log4(4x+1)-x-b没有零点,此时函数y=f(x)的图象与直线y=
| 1 |
| 2 |
综上所述,b≤0时,函数y=f(x)的图象与直线y=
| 1 |
| 2 |
(3)∵g(x)=log4(a•2x-a•m),∴a≠0,
函数f(x)与g(x)的图象有且只有一个公共点
即方程 log4(4x+1)-
| 1 |
| 2 |
化简得:方程 2x+
| 1 |
| 2x |
令t=2x>0,m=
| 4 |
| 3 |
| 1 |
| t |
| 4 |
| 3 |
①当a=1时,t=-
| 3 |
| 4 |
②当a≠1时,△=0⇒a=
| 3 |
| 4 |
若a=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
③若一个正根和一个负根,则
| -1 |
| a-1 |
所以实数a的取值范围为{a|a>1或a=-3}.
点评:本题主要考查了偶函数的性质,以及对数函数图象与性质的综合应用,同时考查了分类讨论的思想,由于综合考查了多个函数的难点,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知关于x的不等式
-
>0的解集为(-∞,-2)∪(1,2),则关于x的不等式
-
>0的解集为( )
| x+a |
| x+b |
| x+c |
| x+d |
| alnx-1 |
| blnx-1 |
| clnx-1 |
| dlnx-1 |
A、(-1,-
| ||||||||
B、(
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,
|
已知cos(
+α)=-
,且α为第四象限角,则cos(-3π+α)=( )
| 3π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
A、y=ln
| ||
| B、y=x3 | ||
| C、y=2|x| | ||
D、y=x
|
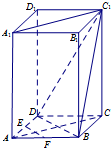 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点. 在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.