题目内容
已知函数f（x）是奇函数，且满足f（x+4）=f（x），当0≤x≤1时，f（x）=x，求f（7.5）．
考点：抽象函数及其应用,函数的值
专题：函数的性质及应用
分析：由题意得到f（7.5）=f（8-0.5）=f（-0.5），再根据函数为奇函数，即而求出值．
解答：
解：∵f（x+4）=f（x），
∴f（x）是以4为周期的周期函数，
∵f（x）是奇函数，
∴f（-x）=-f（x），
设-≤x≤0，则0≤-x≤1，
∴f（-x）=-x=-f（x），
∴f（x）=x，
∴f（7.5）=f（8-0.5）=f（-0.5）=-0.5．
∴f（x）是以4为周期的周期函数，
∵f（x）是奇函数，
∴f（-x）=-f（x），
设-≤x≤0，则0≤-x≤1，
∴f（-x）=-x=-f（x），
∴f（x）=x，
∴f（7.5）=f（8-0.5）=f（-0.5）=-0.5．
点评：本题主要考查抽象函数的周期性来转化区间，属于基础题．
练习册系列答案
相关题目
已知偶函数f（x）在[0，π]上是增函数，那么f（-π），f（-
），f（log2
）之间的大小关系（ ）
| π |
| 2 |
| 1 |
| 4 |
A、f（-π）＞f（log2
| ||||
B、f（-π）＞f（-
| ||||
C、f（log2
| ||||
D、f（-
|
用数学归纳法证明3k≥n3（n≥3，n∈N）第一步应验证（ ）
| A、n=1 | B、n=2 |
| C、n=3 | D、n=4 |
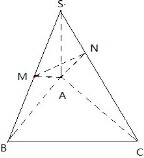在三棱锥S-ABC中，SA⊥底面ABC，∠ABC=90°，且SA=AB，点M是SB的中点，AN⊥SC且交SC于点N．