题目内容
5.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=$\frac{\sqrt{3}}{2}$,则二面角B-AC-D的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 如图所示,在菱形ABCD中,对角线AC∩BD=O,由△ABC与△ACD都为等边三角形,AB=1.可得AC⊥BD,OB=OD=$\frac{\sqrt{3}}{2}$,因此折起后∠BOD是二面角B-AC-D的平面角.利用等边三角形的性质即可得出结论.
解答 解:如图所示,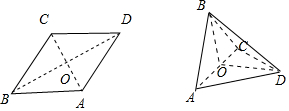
在菱形ABCD中,对角线AC∩BD=O,
由△ABC与△ACD都为等边三角形,AB=1.
∴AC⊥BD,OB=OD=$\frac{\sqrt{3}}{2}$,
∴折起后∠BOD是二面角B-AC-D的平面角.
又BD=$\frac{\sqrt{3}}{2}$,
∴△BOD是等边三角形,
∴∠BOD=$\frac{π}{3}$.
∴sin∠BOD=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查了菱形与等边三角形的性质、二面角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{15}{32}$ | C. | $\frac{11}{32}$ | D. | $\frac{5}{16}$ |
13.命题p:?x0∈R,x0>1的否定是( )
| A. | ¬p:?x∈R,x≤1 | B. | ¬p:?x∈R,x≤1 | C. | ¬p:?x∈R,x<1 | D. | ¬p:?x∈R,x<1 |
17.已知集合A={x|x≤-1或x≥1},B={x|a<x<a+1},且A∩B=B,则实数a的取值范围是( )
| A. | a≤-2 | B. | a≥1 | C. | -2≤a≤1 | D. | a≤-2或a≥1 |