题目内容
14.已知抛物线y2=4x的焦点为F,点P,Q(异于顶点O)在抛物线上.(1)若点P(1,2),试求过点P且与抛物线相切的直线方程;
(2)若过点P,Q且与抛物线分别相切的直线交于点M,证明:|PF|,|MF|,|QF|依次成等比数列.
分析 (1)求导数,确定切线的斜率,可得切线方程;
(2)求出过点P,Q且与抛物线分别相切的直线方程,可得M的坐标,利用等比数列的定义进行证明.
解答 (1)解:由题意,y=2$\sqrt{x}$,y′=$\frac{1}{\sqrt{x}}$,x=1,y′=1,
∴过点P且与抛物线相切的直线方程为y-2=x-1,即x-y+1=0;
(2)证明:设P(x1,y1),Q(x2,y2),则过P的切线方程为y-y1=$\frac{1}{\sqrt{{x}_{1}}}$(x-x1),即y=$\frac{1}{\sqrt{{x}_{1}}}$x+$\sqrt{{x}_{1}}$,
同理过Q的切线方程为y=$\frac{1}{\sqrt{{x}_{2}}}$x+$\sqrt{{x}_{2}}$,可得M($\sqrt{{x}_{1}{x}_{2}}$,$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$),
∴|PF|=x1+1,|QF|=x2+1,|MF|2=($\sqrt{{x}_{1}{x}_{2}}$-1)2+($\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$)2,
∴|MF|2=|PF||QF|,
∴|PF|,|MF|,|QF|依次成等比数列.
点评 本题考查抛物线的切线方程,考查等比数列的证明,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=$\frac{\sqrt{3}}{2}$,则二面角B-AC-D的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.一个几何体的三视图如图所示,则该几何体的体积为( )
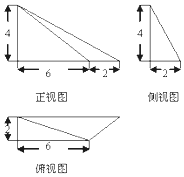

| A. | $\frac{56}{3}$ | B. | $\frac{112}{3}$ | C. | $\frac{119}{3}$ | D. | $\frac{128}{3}$ |
19.命题“若(a-2)(b-3)=0,则a=2或b=3”的否命题是( )
| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
3.函数f(x)=x2-2x+4(x∈[0,3])的值域为( )
| A. | [3,4] | B. | [4,7] | C. | [3,7] | D. | [1,7] |