题目内容
17.已知集合A={x|x≤-1或x≥1},B={x|a<x<a+1},且A∩B=B,则实数a的取值范围是( )| A. | a≤-2 | B. | a≥1 | C. | -2≤a≤1 | D. | a≤-2或a≥1 |
分析 根据A与B的交集为B,得到B为A的子集,即可确定出a的范围.
解答 解:∵A∩B=B,
∴B⊆A,
∵A={x|x≤-1或x≥1},B={x|a<x<a+1},
∴a+1≤-1或a≥1,
解得a≤-2或a≥1,
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$则目标函数z=3x-4y的最大值为( )
| A. | -8 | B. | -6 | C. | -9 | D. | 6 |
8.已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题不正确的是( )
| A. | 若 m∥n,m⊥α,则 n⊥α | B. | 若m∥α,α∩β=n则 m∥n | ||
| C. | 若m⊥β,m⊥α,则α∥β | D. | m⊥α,m?β,则α⊥β |
5.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=$\frac{\sqrt{3}}{2}$,则二面角B-AC-D的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.一个几何体的三视图如图所示,则该几何体的体积为( )
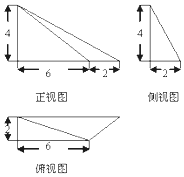

| A. | $\frac{56}{3}$ | B. | $\frac{112}{3}$ | C. | $\frac{119}{3}$ | D. | $\frac{128}{3}$ |