题目内容
16.已知直线l:y=kx(k>0),圆C1:(x-1)2+y2=1与C2:(x-3)2+y2=1,若直线l被圆C1,C2所截得两弦的长度之比是3,则实数k=$\frac{1}{3}$.分析 分别求出弦长,利用直线l被圆C1,C2所截得两弦的长度之比是3,建立方程,即可求出实数k.
解答 解:由题意,圆C1:(x-1)2+y2=1的圆心(1,0)到直线l:y=kx(k>0)的距离=$\frac{k}{\sqrt{{k}^{2}+1}}$,
弦长为2$\sqrt{1-\frac{{k}^{2}}{{k}^{2}+1}}$=$\frac{2}{\sqrt{{k}^{2}+1}}$,
圆C2:(x-3)2+y2=1的圆心(3,0)到直线l:y=kx(k>0)的距离=$\frac{3k}{\sqrt{{k}^{2}+1}}$,
弦长为2$\sqrt{1-\frac{9{k}^{2}}{{k}^{2}+1}}$=$\frac{2\sqrt{1-8{k}^{2}}}{\sqrt{{k}^{2}+1}}$,
∵直线l被圆C1,C2所截得两弦的长度之比是3,
∴$\frac{2}{\sqrt{{k}^{2}+1}}$=3×$\frac{2\sqrt{1-8{k}^{2}}}{\sqrt{{k}^{2}+1}}$,
∴k=$±\frac{1}{3}$.
∵k>0
∴k=$\frac{1}{3}$
故答案为$\frac{1}{3}$.
点评 本题考查直线的斜率的求法,是中档题,解题时要认真审题,注意圆的性质和点到直线的距离公式的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9.某三棱锥的三视图如图所示,该三棱锥的体积是( )
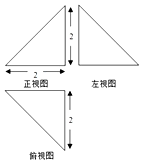

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $6+2\sqrt{3}$ |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$则目标函数z=3x-4y的最大值为( )
| A. | -8 | B. | -6 | C. | -9 | D. | 6 |
8.已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题不正确的是( )
| A. | 若 m∥n,m⊥α,则 n⊥α | B. | 若m∥α,α∩β=n则 m∥n | ||
| C. | 若m⊥β,m⊥α,则α∥β | D. | m⊥α,m?β,则α⊥β |
5.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=$\frac{\sqrt{3}}{2}$,则二面角B-AC-D的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |