题目内容
18.五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{15}{32}$ | C. | $\frac{11}{32}$ | D. | $\frac{5}{16}$ |
分析 求出基本事件的个数,即可求出没有相邻的两个人站起来的概率.
解答 解:五个人的编号为1,2,3,4,5.
由题意,所有事件,共有25=32种,没有相邻的两个人站起来的基本事件有(1),(2),(3),(4),(5),(1,3),(1,4),(2,4),(2,5),(3,5),再加上没有人站起来的可能有1种,共11种情况,
∴没有相邻的两个人站起来的概率为$\frac{11}{32}$,
故选:C.
点评 本题考查没有相邻的两个人站起来的概率,考查列举法的运用,比较基础.

练习册系列答案
相关题目
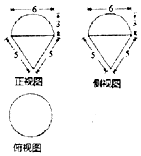
9.某三棱锥的三视图如图所示,该三棱锥的体积是( )

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $6+2\sqrt{3}$ |
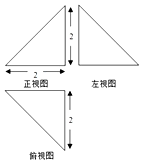
6. 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )| A. | $\frac{19π}{3}$ | B. | $\frac{22π}{3}$ | C. | 19π | D. | 22π |
13.复数(1+i)2+$\frac{2}{1+i}$的共轭复数是( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
3.近年来,我国电子商务蓬勃发展.2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的2×2列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满
意的次数为随机变量X,求X的分布列和数学期望EX.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d为样本容量)
(Ⅰ) 根据已知条件完成下面的2×2列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
| 对服务满意 | 对服务不满意 | 合计 | |
| 对商品满意 | 80 | ||
| 对商品不满意 | |||
| 合计 | 200 |
意的次数为随机变量X,求X的分布列和数学期望EX.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d为样本容量)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≥0\\ 2x-5y+10≤0\\ x+y-4≤0\end{array}\right.$则目标函数z=3x-4y的最大值为( )
| A. | -8 | B. | -6 | C. | -9 | D. | 6 |
5.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=$\frac{\sqrt{3}}{2}$,则二面角B-AC-D的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |