题目内容
已知函数f（x）=lg（x2-4x+8），x∈[0，3]，求函数的最大值和最小值．
考点：对数函数的值域与最值
专题：函数的性质及应用
分析：利用换元法设t=x2-4x+8=（x-2）2+4求出t的取值范围，利用对数函数的单调性即可求出函数的最值．
解答：
解：设t=x2-4x+8=（x-2）2+4，
∵x∈[0，3]，
∴t∈[4，8]，
∴函数y=lgt，在t=4时，取得最小值lg4，
当t=8时，取得最大值lg8．
故当x∈[0，3]，函数的最大值为lg8，最小值为lg4．
∵x∈[0，3]，
∴t∈[4，8]，
∴函数y=lgt，在t=4时，取得最小值lg4，
当t=8时，取得最大值lg8．
故当x∈[0，3]，函数的最大值为lg8，最小值为lg4．
点评：本题主要考查函 数最值的计算，利用二次函数和对数函数的性质是解决本题的关键，比较基础．
练习册系列答案
相关题目
若双曲线
-
=1（a＞0，b＞0）的渐近线方程式y=±
x，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
在复平面内，复数
对应的点位于（ ）
| 2i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
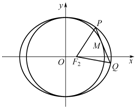已知椭圆
如图，焦点在x轴上的椭圆T1与焦点在y轴上的椭圆T2相切于点M（0，1），且椭圆T1与T2的离心率均为
如图，在Rt△ABC中，∠BAC、∠ABC、∠ACB成等差数列，且AB=4，D点是斜边BC上一动点，连接AD，以AD为折痕，将△ABD折到与△ADC的同一个平面内，B变为B1，设∠BAD=θ．