题目内容
9.下列命题成立的是( )| A. | 若¬p、¬q均为真命题,则p∨q为真命题 | |
| B. | 命题“若x2+2x<0,则-2<x<0”的逆否命题为“若-2<x<0,则x2+2x<0” | |
| C. | 方程x2=1的一个必要不充分条件是x=1 | |
| D. | 抛掷3枚质地均匀的硬币,事件“至少有两枚硬币正面向上”等价于“至多有一枚硬币反面向上” |
分析 A,若¬p、¬q均为真命题,则p、q均为假命题,则p∨q为假命题;
B,命题“若x2+2x<0,则-2<x<0”的逆否命题为“若x≤-2或x≥0,则x2+2x≥0”;
C,方程x2=1的一个充分不必要条件是x=1;
D,列举出所有情况,看正面都同时向上的情况数占总情况数的多少即可.
解答 解:对于A,若¬p、¬q均为真命题,则p、q均为假命题,则p∨q为假命题,故错;
对于B,命题“若x2+2x<0,则-2<x<0”的逆否命题为“若x≤-2或x≥0,则x2+2x≥0”,故错;
对于C,方程x2=1的一个充分不必要条件是x=1,故错;
对于D,抛掷3枚质地均匀的硬币,列举出所有情况,事件“至少有两枚硬币正面向上”等价于“至多有一枚硬币反面向上”,正确;
故选:D.
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若动点A(x1,y1)、B(x2,y2)分别在直线l1:2x-y+11=0和l2:2x-y-1=0上移动,则AB的中点M所在的直线方程为( )
| A. | 2x+y-5=0 | B. | 2x+y+5=0 | C. | 2x-y-5=0 | D. | 2x-y+5=0 |
17.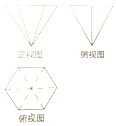 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
14.为了得到函数y=1-2sin2(x-$\frac{π}{12}$)的图象,可以将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
1.101(9)化为十进制数为( )
| A. | 9 | B. | 11 | C. | 82 | D. | 101 |
19.过点(1,2),且与原点距离最大的直线方程是( )
| A. | x+2y-5=0 | B. | 2x+y-4=0 | C. | x+3y-7=0 | D. | x-2y+3=0 |