题目内容
5.将正整数12分解成两个正整数的乘积有1×12,2×6,3×4三种,其中3×4是这三种分解中两数差的绝对值最小的,我们称3×4为12的最佳分解.当p×q(p≤q且pq∈N*,)是正整数n的最佳分解时,我们定义函数f(n)=q-p,例如f(12)=4-3=1.数列{f(3n)}的前100项和为350-1.分析 当n为偶数时,f(3n)=0;当n为奇数时,f(3n)=${3}^{\frac{n+1}{2}}$-${3}^{\frac{n-1}{2}}$=2×${3}^{\frac{n-1}{2}}$,再利用等比数列的求和公式即可得出.
解答 解:当n为偶数时,f(3n)=0;
当n为奇数时,f(3n)=${3}^{\frac{n+1}{2}}$-${3}^{\frac{n-1}{2}}$=2×${3}^{\frac{n-1}{2}}$,
∴S100=2(30+31+…+349)=$2×\frac{{3}^{50}-1}{3-1}$=350-1.
故答案为:350-1.
点评 本题考查了等比数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.六安滨河公园喷泉中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在水柱正西方向的A处测得水柱顶端的仰角为45°,沿A处向南偏东30°前进50米到达点B处,在B处测得水柱顶端的仰角为30°,则水柱的高度是( )
| A. | 15m | B. | 30m | C. | 25m | D. | 50m |
17.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}<1$”是“a>1”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | 设随机变量X~N(1,52),若P(X<0)=P(X>a-2),则实数a的值为2 |
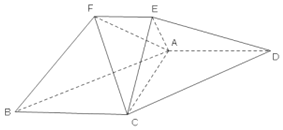 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,