题目内容
17.下列说法正确的是( )| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}<1$”是“a>1”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | 设随机变量X~N(1,52),若P(X<0)=P(X>a-2),则实数a的值为2 |
分析 判断逆否命题的真假,可得原命题的真假;根据充要条件的定义,可判断B;写出原命题的否定,可判断C;根据正态分布的对称性,可判断D.
解答 解:若x+y≠0,则x≠1且y≠-1的逆否命题为“若x=1,或y=-1,则x+y=0”为假命题,故原命题为假命题,故A错误;
“$\frac{1}{a}<1$”?“a<0,或a>1”,故“$\frac{1}{a}<1$”是“a>1”的必要不充分条件,故B正确;
命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3≥0”,故C错误;
设随机变量X~N(1,52),若P(X≤0)=P(X>a-2),则a-2=2,则实数a的值为4,故D错误;
故选:B.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,充要条件,命题的否定,正态分布等知识点,难度中档.

练习册系列答案
相关题目
7.等比数列{an}的前n项和为Sn,已知a2a5=2a3,且a4与2a7的等差中项为$\frac{5}{4}$,则S4=( )
| A. | 29 | B. | 30 | C. | 33 | D. | 36 |
2.大数据时代出现了滴滴打车服务,二胎政策的放开使得家庭中有两个小孩的现象普遍存在,某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,准备使用滴滴打车软件,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
9.阅读下边的程序框图,运行相应的程序,若输出S的值为16,则输入m的值可以为( )
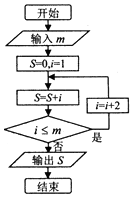

| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
6.若集合A={x|log4x≤$\frac{1}{2}$},B={x|(x+3)( x-1)≥0},则A∩(∁RB)=( )
| A. | (0,1] | B. | (0,1) | C. | [1,2] | D. | [0,1] |
18.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直x轴的直线交C于A,B两点,且|AB|=3,则C的方程为( )
| A. | $\frac{x^2}{2}$+y2=1 | B. | $\frac{x^2}{3}$+$\frac{y^2}{2}$=1 | C. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 | D. | $\frac{x^2}{5}$+$\frac{y^2}{4}$=1 |