题目内容
6.化简下列各式:(1)sin2αcos2α+cos4α+sin2α;
(2)$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$(α为第二象限角).
分析 (1)利用cos2α+sin2α=1即可化简求值;
(2)把根式内部采用分母有理化,开方后结合角α的范围得答案.
解答 解:(1)sin2αcos2α+cos4α+sin2α=cos2α(cos2α+sin2α)+sin2α=cos2α+sin2α=1;
(2)$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=$\frac{1+sinα}{|cosα|}-\frac{1-sinα}{|cosα|}=\frac{2sinα}{|cosα|}$,
∵α为第二象限角,∴cosα<0.
则$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=-2tanα.
点评 本题主要考查了同角三角函数基本关系式的应用,灵活应用cos2α+sin2α=1是解题的关键,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6.若集合A={x|log4x≤$\frac{1}{2}$},B={x|(x+3)( x-1)≥0},则A∩(∁RB)=( )
| A. | (0,1] | B. | (0,1) | C. | [1,2] | D. | [0,1] |
3.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线$y=-\sqrt{3}x$上,则sin2θ=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
1.已知直线y=ax是曲线y=lnx的切线,则实数a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{{e}^{2}}$ |
11.已知全集U=R,M={x|y=lg(1-$\frac{2}{x}$)},N={x|y=$\sqrt{x-1}$},则N∩(∁UM)=( )
| A. | ∅ | B. | [1,2] | C. | [0,2] | D. | [2,+∞) |
18.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直x轴的直线交C于A,B两点,且|AB|=3,则C的方程为( )
| A. | $\frac{x^2}{2}$+y2=1 | B. | $\frac{x^2}{3}$+$\frac{y^2}{2}$=1 | C. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 | D. | $\frac{x^2}{5}$+$\frac{y^2}{4}$=1 |
15.设数列{an}的通项公式an=ncos$\frac{nπ}{3}$,其前n项和为Sn,则S2016=( )
| A. | 2016 | B. | -2016 | C. | 1008 | D. | -1008 |
16.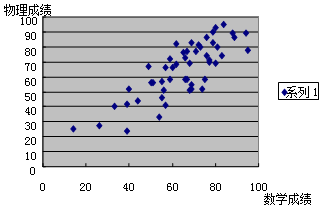 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )
在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到如下散点图,用回归直线$\hat y=bx+a$近似刻画其关系,根据图形,b的数值最有可能是( )| A. | 0 | B. | 1.55 | C. | 0.45 | D. | -0.24 |