题目内容
已知f(x)是偶函数,且在[0,+∞)上是减函数,若f(lgx)>f(2),则x的取值范围是 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系将不等式进行转化即可得到结论.
解答:
解:∵f(x)是偶函数,且在[0,+∞)上是减函数,
∴不等式f(lgx)>f(2)等价为f(|lgx|)>f(2),
即|lgx|<2,
即-2<lgx<2,
解得
<x<10,
故不等式的解集为(
,10),
故答案为:(
,10)
∴不等式f(lgx)>f(2)等价为f(|lgx|)>f(2),
即|lgx|<2,
即-2<lgx<2,
解得
| 1 |
| 10 |
故不等式的解集为(
| 1 |
| 10 |
故答案为:(
| 1 |
| 10 |
点评:本题主要考查不等式的求解,利用奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x,y如下表所示,若x和y线性相关,
且线性回归直线方程是
=bx+2.4,则b=( )
| x | 1 | 2 | 3 | 4 | 5 |
| y[ | 2.9 | 3.7 | 4.5 | 5.3 | 6.1 |
| ? |
| y |
| A、0.7 | B、0.8 |
| C、0.9 | D、1 |
若函数f(x)=x3-6ax+5在区间(2,+∞)内是增函数;则实数a的取值范围是( )
| A、a∈(-∞,4] |
| B、a∈(-∞,2] |
| C、a∈[2,+∞) |
| D、a∈[4,+∞) |
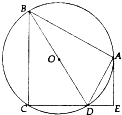 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA. 求曲线y=sinx,y=cosx与直线x=0,x=
求曲线y=sinx,y=cosx与直线x=0,x=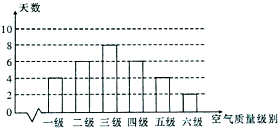 根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表: