题目内容
已知直线l经过A(4,0)、B(0,3),求直线l1的一般方程,使得:
(1)l1∥l,且经过两直线3x+y=0与x+y=2交点;
(2)l1⊥l,且与两坐标轴围成的三角形的面积为6.
(1)l1∥l,且经过两直线3x+y=0与x+y=2交点;
(2)l1⊥l,且与两坐标轴围成的三角形的面积为6.
考点:直线的截距式方程
专题:直线与圆
分析:(1)联立
,解得交点C(-1,3).由截距式可得直线l的方程为
+
=1,设直线l1的方程为
+
=m.把C代入即可.
(2)设直线l1的方程为
-
=n,当x=0时,y=-4n;当y=0时,x=3n.直线l1与两坐标轴围成的三角形的面积为S=
|3n|•|-4n|=6,解得即可.
|
| x |
| 4 |
| y |
| 3 |
| x |
| 4 |
| y |
| 3 |
(2)设直线l1的方程为
| x |
| 3 |
| y |
| 4 |
| 1 |
| 2 |
解答:
解:(1)联立
,解得
,即交点C(-1,3).
直线l的方程为
+
=1,
设直线l1的方程为
+
=m.
∵直线l1经过两直线的交点C(-1,3),
∴m=
+
=
.
故直线l1的方程为
+
=
,即3x+4y-9=0.
(2)设直线l1的方程为
-
=n,
当x=0时,y=-4n;当y=0时,x=3n.
直线l1与两坐标轴围成的三角形的面积为S=
|3n|•|-4n|=6,即n2=1.
解得n=±1.
故直线l1的方程为
-
=±1,即4x-3y-12=0或4x-3y+12=0.
|
|
直线l的方程为
| x |
| 4 |
| y |
| 3 |
设直线l1的方程为
| x |
| 4 |
| y |
| 3 |
∵直线l1经过两直线的交点C(-1,3),
∴m=
| -1 |
| 4 |
| 3 |
| 3 |
| 3 |
| 4 |
故直线l1的方程为
| x |
| 4 |
| y |
| 3 |
| 3 |
| 4 |
(2)设直线l1的方程为
| x |
| 3 |
| y |
| 4 |
当x=0时,y=-4n;当y=0时,x=3n.
直线l1与两坐标轴围成的三角形的面积为S=
| 1 |
| 2 |
解得n=±1.
故直线l1的方程为
| x |
| 3 |
| y |
| 4 |
点评:本题考查了直线的截距式、相互平行与垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知x,y如下表所示,若x和y线性相关,
且线性回归直线方程是
=bx+2.4,则b=( )
| x | 1 | 2 | 3 | 4 | 5 |
| y[ | 2.9 | 3.7 | 4.5 | 5.3 | 6.1 |
| ? |
| y |
| A、0.7 | B、0.8 |
| C、0.9 | D、1 |
已知集合D={x|
>0},若a,b∈D且
+
=
,则9a•3b的最小值为( )
| 24-x |
| x-9 |
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 12 |
| A、27 |
| B、327 |
| C、54 |
| D、354 |
设全集为I,则表示右图中阴影部分的集合是( )


| A、A∪B |
| B、A∩B |
| C、(∁IA)∪(∁IB) |
| D、(∁IA)∩(∁IB) |
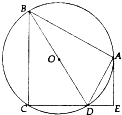 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA. 根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表: