题目内容
若α+β=
，则sinα-sin（
+β）= ．
| π |
| 2 |
| π |
| 2 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式化简要求式子的值，可得结果．
解答：
解：若α+β=
，则sinα-sin（
+β）=sinα-sin（π-α）=sinα-sinα=0，
故答案为：0．
| π |
| 2 |
| π |
| 2 |
故答案为：0．
点评：本题主要考查应用诱导公式化简三角函数式，要特别注意符号的选取，这是解题的易错点，属于基础题．
练习册系列答案
学业测评一课一测系列答案
相关题目
设函数f（x）是（-∞，+∞）上的减函数，又若a∈R，则（ ）
| A、f （a）＞f（2a） |
| B、f （a2）＜f（a） |
| C、f （a2+a）＜f（a） |
| D、f（a2+1）＜f（a） |
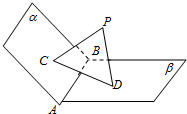如图，已知平面α，β，且α∩β=AB，PC⊥α，PD⊥β，C，D是垂足．且PC=PD=CD=1，则二面角α-AB-β的大小是（ ）| A、120° | B、45° |
| C、60° | D、150° |
已知向量
、
、
是单位向量，且
•
=0，则（
-
）•（
-
）的最大值为（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
A、
| ||
B、2+
| ||
C、
| ||
D、
|