题目内容
 如图所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求三棱柱ABC-A′B′C′的体积.
如图所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求三棱柱ABC-A′B′C′的体积.考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,可得V四棱锥A′-BCC′B′=
a•S.又V三棱锥A′-ABC=
V三棱柱ABC-A′B′C′.可得V四棱锥A′-BCC′B′+V三棱锥A′-ABC=V三棱柱ABC-A′B′C′.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:∵侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,
∴V四棱锥A′-BCC′B′=
a•S.
∵V三棱锥A′-ABC=
V三棱柱ABC-A′B′C′.
∵V四棱锥A′-BCC′B′+V三棱锥A′-ABC=V三棱柱ABC-A′B′C′.
∴
aS=
V三棱柱ABC-A′B′C′.
∴V三棱柱ABC-A′B′C′=
aS.
∴V四棱锥A′-BCC′B′=
| 1 |
| 3 |
∵V三棱锥A′-ABC=
| 1 |
| 3 |
∵V四棱锥A′-BCC′B′+V三棱锥A′-ABC=V三棱柱ABC-A′B′C′.
∴
| 1 |
| 3 |
| 2 |
| 3 |
∴V三棱柱ABC-A′B′C′=
| 1 |
| 2 |
点评:本题考查了棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知x>0,y>0,且4x+y=1,则
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
| A、9 | B、8 | C、7 | D、6 |
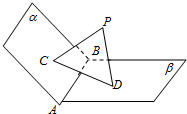 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )| A、120° | B、45° |
| C、60° | D、150° |
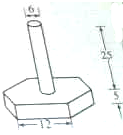 如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).
如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).