题目内容
把半径为2的四个小球垒成两层放在桌子上，下层放3个，上层放1个，两两相切．求上层的最高点离桌面的距离．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：设四个球的球心分别为O1、O2、O3、O4，将它们两两连结恰好组成一个正三棱锥，且各棱长均为2R，作O1H⊥面O2O3O4，垂足为H，则O1H为棱锥的高，由此可求上面一个球的球心到桌面的距离．
解答：
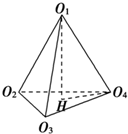解：设四个球的球心分别为O1、O2、O3、O4，将它们两两连结恰好组成一个正三棱锥，且各棱长均为4，作O1H⊥面O2O3O4，垂足为H，则O1H为棱锥的高．
连接O4H，则O4H=
，
∵O1H⊥面O2O3O4，
∴O1H⊥HO4，即∠O1HO4=90°，∴O1H=
=
=
，
则从上面一个球的球心到桌面的距离为
+2．
上层的最高点离桌面的距离：
+4．
解：设四个球的球心分别为O1、O2、O3、O4，将它们两两连结恰好组成一个正三棱锥，且各棱长均为4，作O1H⊥面O2O3O4，垂足为H，则O1H为棱锥的高．连接O4H，则O4H=
4
| ||
| 3 |
∵O1H⊥面O2O3O4，
∴O1H⊥HO4，即∠O1HO4=90°，∴O1H=
| O1O42-O4H2 |
42-(
|
4
| ||
| 3 |
则从上面一个球的球心到桌面的距离为
4
| ||
| 3 |
上层的最高点离桌面的距离：
4
| ||
| 3 |
点评：本题考查点到面的距离的计算，考查学生分析解决问题的能力，考查学生转化问题的能力，属于中档题．
练习册系列答案
相关题目
已知a=0.5-
，b=(
)-
，c=log2.51.5，则a，b，c的大小关系（ ）
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 3 |
| A、c＜a＜b |
| B、c＜b＜a |
| C、a＜b＜c |
| D、b＜a＜c |
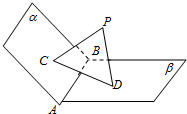如图，已知平面α，β，且α∩β=AB，PC⊥α，PD⊥β，C，D是垂足．且PC=PD=CD=1，则二面角α-AB-β的大小是（ ）| A、120° | B、45° |
| C、60° | D、150° |
已知向量
、
、
是单位向量，且
•
=0，则（
-
）•（
-
）的最大值为（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
A、
| ||
B、2+
| ||
C、
| ||
D、
|