题目内容
15．关于x的不等式|x+1|+|x-3|＜a的解集包含（1，4），则实数a的取值范围是（6，+∞）．分析 由条件利用绝对值的意义，求得a的范围．
解答 解：根据|x+1|+|x-3|表示数轴上的点x到-1、3对应点的距离之和，
1对应点到-1、3对应点的距离之和等于4，而4对应点到-1、3对应点的距离之和等于6，
关于x的不等式|x+1|+|x-3|＜a的解集包含（1，4），故a＞6，
故答案为：（6，+∞）．
点评 本题主要考查绝对值不等式的解法，绝对值的意义，属于基础题．
练习册系列答案
相关题目
5．在区间[-5，5]内随机地取出一个数a，使得1∈{x|2x2+ax-a2＞0}的概率为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{3}{20}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{2}$ |
6．命题“若x=1，则x2=1”的否命题是（ ）
| A． | 若x=1，则x2≠1 | B． | 若x≠1，则x2=1 | C． | 若x≠1，则x2≠1 | D． | 若x2≠1，则x≠1 |
3．下列函数中，周期为π，且在（$\frac{π}{4}$，$\frac{π}{2}$）上单调递减的是（ ）
| A． | y=sinxcosx | B． | y=sinx+cosx | C． | y=tan（x+$\frac{π}{4}$） | D． | y=2cos22x-1 |
10．
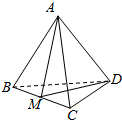如图所示的正四面体A-BCD中，截面ADM将其分成体积相等的两部分，则AB与截面ADM所成角为（ ）
如图所示的正四面体A-BCD中，截面ADM将其分成体积相等的两部分，则AB与截面ADM所成角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 无法确定 |
7．如图是一个几何体的三视图．则该几何体的体积为（ ）
| A． | 6π | B． | 8π | C． | 12π | D． | 24π |
4．若全集U=R，集合A={x|0＜x＜2}，B={x|x-1＞0}，则A∩∁UB=（ ）
| A． | {x|0＜x≤1} | B． | {x|1＜x＜2} | C． | {x|0＜x＜1} | D． | {x|1≤x＜2} |
18．已知A（0，-2），B（3，2）是函数f（x）图象上的两点，且f（x）是R上的增函数，则|f（x）|＜2的解集为（ ）
| A． | （1，4） | B． | （-1，2） | C． | （0，3） | D． | （3，4） |