题目内容
正方体ABCD-A1B1C1D1中,平面D1B1A和平面C1DB的位置关系是 .
考点:平面与平面之间的位置关系
专题:证明题,空间位置关系与距离
分析:根据正方体中相应的对角线之间的平行关系,我们易得到平面AB1D1和平面BC1D内有两个相交直线相互平行,由面面平行的判定定理,我们易得到平面AB1D1和平面BC1D的位置关系.
解答:
解:∵AB1∥C1D,AD1∥BC1,
AB1?平面AB1D1,AD1?平面AB1D1,AB1∩AD1=A,
C1D?平面BC1D,BC1?平面BC1D,C1D∩BC1=C1,
由面面平行的判定理我们易得平面AB1D1∥平面BC1D,
故答案为:平行.
AB1?平面AB1D1,AD1?平面AB1D1,AB1∩AD1=A,
C1D?平面BC1D,BC1?平面BC1D,C1D∩BC1=C1,
由面面平行的判定理我们易得平面AB1D1∥平面BC1D,
故答案为:平行.
点评:本题考查的知识点是平面与平面之间的位置关系,在判断线与面的平行与垂直关系时,正方体是最常用的空间模型,大家一定要熟练掌握这种方法.

练习册系列答案
相关题目
过抛物线y2=10x的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线( )
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
若x、y满足约束条件
目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
|
| A、(-4,2) |
| B、(-1,2) |
| C、(-4,0) |
| D、(-2,4) |
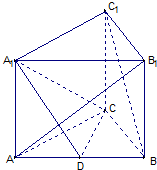 如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.
如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.