题目内容
18．
阅读右边的程序框图，运行相应程序，输出s的值为87．
分析 模拟程序的运行，依次写出每次循环得到的s，k的值，当k=8时满足条件k＞7，退出循环，输出s的值为87．
解答 解：模拟程序的运行，可得
s=1，k=4
执行循环体，s=6，k=5
不满足条件k＞7，执行循环体，s=17，k=6
不满足条件k＞7，执行循环体，s=40，k=7
不满足条件k＞7，执行循环体，s=87，k=8
满足条件k＞7，退出循环，输出s的值为87．
故答案为：87．
点评 本题主要考查了循环结构的程序框图的应用，当循环的次数有限，或有规律时常采用模拟程序运行的方法解决，属于基础题．
练习册系列答案
相关题目
8．已知$a={log_3}\frac{1}{2}$，$b={log_{\frac{1}{2}}}\frac{1}{3}$，$c={（\frac{1}{2}）^{\frac{1}{3}}}$，则（ ）
| A． | c＞b＞a | B． | b＞c＞a | C． | b＞a＞c | D． | c＞a＞b |
9．
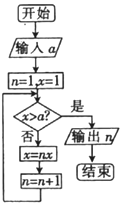执行如图所示程序框图，若输出的结果为5，则输入的实数a的范围是（ ）
执行如图所示程序框图，若输出的结果为5，则输入的实数a的范围是（ ）| A． | [6，24） | B． | [24，120） | C． | （-∞，6） | D． | （5，24） |
6．为了政府对过热的房地产市场进行调控决策，统计部门对城市人和农村人进行了买房心理预测调研，用简单随机抽样的方法抽取了110人进行统计，得到如下列联表：
已知样本中城市人数与农村人数之比是3：8．
（Ⅰ）分别求样本中城市人中的不买房人数和农村人中的纠结人数；
（Ⅱ）从参与调研的城市人中用分层抽样方法抽取6人，进一步统计城市人的某项收入指标，假设一个买房人的指标算作3，一个纠结人的指标算作2，一个不买房人的指标算作1，现在从这6人中再随机选取3人，令X=再抽取3人指标之和，求X的分布列和数学期望．
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
（Ⅰ）分别求样本中城市人中的不买房人数和农村人中的纠结人数；
（Ⅱ）从参与调研的城市人中用分层抽样方法抽取6人，进一步统计城市人的某项收入指标，假设一个买房人的指标算作3，一个纠结人的指标算作2，一个不买房人的指标算作1，现在从这6人中再随机选取3人，令X=再抽取3人指标之和，求X的分布列和数学期望．
13．某象棋俱乐部有队员5人，其中女队员2人，现随机选派2人参加象棋比赛，则选出的2人中恰有1人是女队员的概率为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{3}$ |
3．某机械厂组装A，B两种类型机械，每组装1台A或B所需要的配件材料费和工人数如下表所示．
已知该机械厂现有工人32人，可用资金55万元，组装1台A类型机械可获纯利润4万元，组装1台B类型机械可获纯利润2万元，设该机械厂计划组装A，B两种类型机械分别为x台，y台．
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问该机械厂分别组装A，B两种类型机械各多少台，才能获得最大利润？并求出此最大纯利润．
| 类型 条件 | A | B |
| 配件材料费（万元） | 20 | 5 |
| 工人数（人） | 4 | 8 |
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问该机械厂分别组装A，B两种类型机械各多少台，才能获得最大利润？并求出此最大纯利润．
10．设x∈R，则“|x-2|＜1”是“x2-2x-8＜0”的（ ）
| A． | 充要条件 | B． | 充分而不必要条件 | ||
| C． | 必要而不充分条件 | D． | 既不充分也不必要条件 |
7．若全集U=R，集合A={x|1＜2x＜4}，B={x|x-1≥0}，则A∩（∁UB）（ ）
| A． | {x|1＜x＜2} | B． | {x|0＜x＜1} | C． | {x|0＜x≤1} | D． | {x|1≤x＜2} |