题目内容
已知椭圆
+
=1(a>b>0)与直线l:y=-
x+b交于不同的两点P,Q,原点到该直线的距离为
,且椭圆的离心率为
.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在实数k,使直线y=kx+2交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在实数k,使直线y=kx+2交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由点到直线的距离公式,即可求得b=1,再由离心率公式和a,b,c的关系,即可求得a,进而得到椭圆方程;
(Ⅱ)假设存在实数k,使直线y=kx+2交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0),联立直线方程和椭圆方程,消去y,运用韦达定理,以及PQ⊥QD,即(x1-1)(x2-1)+y1y2=0,又y1=kx1+2,y2=kx2+2,化简整理,解出k,注意检验判别式是否等于0,即可判断.
(Ⅱ)假设存在实数k,使直线y=kx+2交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0),联立直线方程和椭圆方程,消去y,运用韦达定理,以及PQ⊥QD,即(x1-1)(x2-1)+y1y2=0,又y1=kx1+2,y2=kx2+2,化简整理,解出k,注意检验判别式是否等于0,即可判断.
解答:
解:(Ⅰ)由点到直线的距离公式,得d=
=
,
解得:b=1,即a2-c2=1,
又椭圆的离心率为
,即
=
,解得,a=
,
∴椭圆方程是
+y2=1;
(Ⅱ)假设存在实数k,使直线y=kx+2交椭圆于P、Q两点,
以PQ为直径的圆过点D(1,0).
将y=kx+2代入椭圆方程,得,(1+3k2)x2+12kx+9=0,
设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点D(1,0).
则PQ⊥QD,即(x1-1)(x2-1)+y1y2=0,
又y1=kx1+2,y2=kx2+2,得,(1+k2)(x1x2+(2k-1)(x1+x2)+5=0,
又x1+x2=-
,x1x2=
,
代入上式可得,
=0,解得,k=-
.
此时代入△=(12k)2-4×9(1+3k2)>0,
则存在k=-
.使直线y=kx+2交椭圆于P、Q两点,
以PQ为直径的圆过点D(1,0).
| ||
| 2 |
| |b| | ||||
|
解得:b=1,即a2-c2=1,
又椭圆的离心率为
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| 3 |
∴椭圆方程是
| x2 |
| 3 |
(Ⅱ)假设存在实数k,使直线y=kx+2交椭圆于P、Q两点,
以PQ为直径的圆过点D(1,0).
将y=kx+2代入椭圆方程,得,(1+3k2)x2+12kx+9=0,
设P(x1,y1),Q(x2,y2),以PQ为直径的圆过点D(1,0).
则PQ⊥QD,即(x1-1)(x2-1)+y1y2=0,
又y1=kx1+2,y2=kx2+2,得,(1+k2)(x1x2+(2k-1)(x1+x2)+5=0,
又x1+x2=-
| 12k |
| 1+3k2 |
| 9 |
| 1+3k2 |
代入上式可得,
| 12k+14 |
| 1+3k2 |
| 7 |
| 6 |
此时代入△=(12k)2-4×9(1+3k2)>0,
则存在k=-
| 7 |
| 6 |
以PQ为直径的圆过点D(1,0).
点评:本题考查椭圆方程和性质,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理解题,考查直线和圆的位置关系,考查运算能力,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知集合A={x∈R|x≤5},B={x∈R|x>1}那么A∩B等于( )
| A、{1,2,3,4,5} |
| B、{2,3,4,5} |
| C、{2,3,4} |
| D、{x∈R|1<x≤5} |
直三棱柱ABC-EFG所有顶点在半径为
的球面上,AB=AC=
,AE=2,B-AE-C余弦为( )
| 2 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列推理正确的是( )
| A、把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay |
| B、把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny |
| C、把a(b+c)与ax+y类比,则有ax+y=ax+ay |
| D、把a(b+c)与a*(b+c)类比,则有a*(b+c)=a*b+a* |
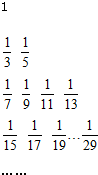 数列{
数列{