题目内容
18.集合M={(x,y)|x+y≤1,y≤x,y≥-1},N={(x,y)|(x-2)2+y2=r2,r>0},若M∩N≠∅,则r的取值范围为( )| A. | $[{\frac{{\sqrt{2}}}{2},3}]$ | B. | $[{1,\sqrt{10}}]$ | C. | $[{\frac{{\sqrt{2}}}{2},\sqrt{10}}]$ | D. | $[{1,\frac{{\sqrt{10}}}{2}}]$ |
分析 由题意画出图形,结合点到直线的距离公式及两点间的距离公式得答案.
解答 解:画出集合M={(x,y)|x+y≤1,y≤x,y≥-1}表示的平面区域如图,
集合N={(x,y)|(x-2)2+y2=r2,r>0}表示以(2,0)为圆心,半径为r的圆.
联立$\left\{\begin{array}{l}{y=x}\\{y=-1}\end{array}\right.$,解得A(-1,-1),
∵点(2,0)到直线x+y-1=0的距离d=$\frac{|1×2-1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
|PA|=$\sqrt{(-1-2)^{2}+(-1-0)^{2}}=\sqrt{10}$.
∴若M∩N≠∅,则r的取值范围为[$\frac{\sqrt{2}}{2},\sqrt{10}$].
故选:C.
点评 本题考查交集及其运算,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
9.我国古代数学名著《九章算术》第三章“衰分”介绍比例分配:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”.如:甲、乙、丙、丁分别得100,60,36,21.6个单位,递减的比例是40%,今共有粮食m(m>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丁分得2石,乙、丙所得之和为40石,则衰分比与m的值分别是( )
| A. | 75%,170 | B. | 75%,340 | C. | 25%,170 | D. | 25%,340 |
6.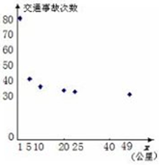 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
把界桩公里数1001记为x=1,公里数1005记为x=5,…,数据绘成的散点图如图所示,以x为解释变量、交通事故数y为预报变量,建立了两个不同的回归方程y(1)=29.9+50.2×$\frac{1}{x}$和y(2)=33.9+125.9e-x表述x,y二者之间的关系.
(Ⅰ)计算R2的值,判断这两个回归方程中哪个拟合效果更好?并解释更好的这个拟合所对R2的意义;
(Ⅱ)若保险公司在每次交通事故中理赔60万元的概率为0.01,理赔2万元的概率为0.19,理赔0.2万元的概率为0.8,利用你得到的拟合效果更好的这一个回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:对回归直线y=$\widehat{α}$+$\widehat{β}$x,有R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$.
一些量的计算值:
表中:${\widehat{{y}_{i}}}^{(1)}$=29.9+50.2×$\frac{1}{{x}_{i}}$,${\widehat{{y}_{i}}}^{(2)}$=33.9+125.9e${\;}^{-{x}_{i}}$,$\frac{1}{40}$=0.025,e-40≈0.
 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
(Ⅰ)计算R2的值,判断这两个回归方程中哪个拟合效果更好?并解释更好的这个拟合所对R2的意义;
(Ⅱ)若保险公司在每次交通事故中理赔60万元的概率为0.01,理赔2万元的概率为0.19,理赔0.2万元的概率为0.8,利用你得到的拟合效果更好的这一个回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:对回归直线y=$\widehat{α}$+$\widehat{β}$x,有R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$.
一些量的计算值:
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
13.执行如图所示的程序框图,则输出的k=( )
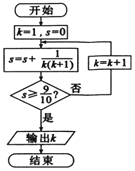

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
10.已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…fn+1(x)=f′n(x),n∈N,那么f2017=( )
| A. | cosx-sinx | B. | sinx-cosx | C. | sinx+cosx | D. | -sinx-cosx |
8.我们常用函数y=f(x)的函数值的改变量与自变量的改变量的比值来表示平均变化率,当自变量x由x0改变到x+x0时,函数值的改变量△y等于( )
| A. | f(x0+△x) | B. | f(x0)+△x | C. | f(x0)•△x | D. | f(x0+△x)-f(x0) |
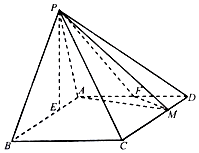 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.