题目内容
1.在△ABC中,∠C=90°,BC=2$\sqrt{3}$,AC=2,M为AB中点,将△ACM沿CM折起,使A、B之间的距离为2$\sqrt{2}$,则三棱锥M-ABC的体积为$\frac{2\sqrt{2}}{3}$.分析 先在原图中作AD⊥MC交MC于点D,交BC于E点,将△ACM沿CM折起后,只要证明AE⊥底面BCM即可.
解答 解:在△ABC中,AB=4,AM=MB=MC=2,
由△AMC为等边三角形,取CM中点D,则AD⊥CM,设AD交BC与E,则AD=$\sqrt{3}$,DE=$\frac{\sqrt{3}}{3}$,CE=$\frac{2\sqrt{3}}{3}$.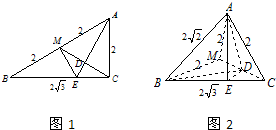
折起后,由BC2=AC2+AB2,知∠BAC=90°,
又cos∠ECA=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$.∴AE2=CA2+CE2-2CA•CEcos∠ECA=$\frac{8}{3}$,
于是AC2=AE2+CE2.∴∠AEC=90°.
∵AD2=AE2+ED2,∴AE⊥DE,
∴AE⊥平面BCM,即AE是三棱锥A-BCM的高,AE=$\frac{2\sqrt{6}}{3}$.
∵S△BCM=$\frac{1}{2}$×$2×2\sqrt{3}×sin30°$=$\sqrt{3}$,
∴VA-BCM=$\frac{1}{3}{S}_{△BCM}•AE$=$\frac{1}{3}×\sqrt{3}×\frac{2\sqrt{6}}{3}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题考查由平面图形折成空间图形求其体积,求此三棱锥的高是解决问题的关键.本题还可以直接过点A作AE⊥BC交BC于E点,连接ME,证明AE⊥ME,即可说明AE⊥底面BCM.

练习册系列答案
相关题目
11.正项等比数列{an}中,存在两项am、an使得$\sqrt{{a_m}•{a_n}}=2{a_1}$,且a6=a5+2a4,则$\frac{1}{m}+\frac{4}{n}$的最小值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{9}{4}$ |
13.下列命题中的假命题是( )
| A. | log23<log35 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ${log_{\frac{1}{2}}}3<{(\frac{1}{2})^3}<{3^{\frac{1}{2}}}$ | D. | ?x>0,x>sinx |
 根据如图所示的伪代码,如果输出y=5,那么输入的x的组成的集合为{-5,5}.
根据如图所示的伪代码,如果输出y=5,那么输入的x的组成的集合为{-5,5}.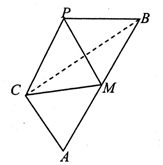 已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.
已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.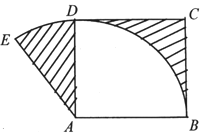 如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.
如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.
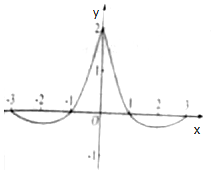 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )