题目内容
11.正项等比数列{an}中,存在两项am、an使得$\sqrt{{a_m}•{a_n}}=2{a_1}$,且a6=a5+2a4,则$\frac{1}{m}+\frac{4}{n}$的最小值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{9}{4}$ |
分析 由a6=a5+2a4,求出公比q,$\sqrt{{a_m}•{a_n}}=2{a_1}$,确定m,n的关系,然后利用基本不等式即可求出$\frac{1}{m}+\frac{4}{n}$的最小值.
解答 解:在等比数列中,∵a6=a5+2a4,
∴a4q2=a4q+2a4,
即q2-q-2=0,
解得q=2或q=-1(舍去),
∵$\sqrt{{a_m}•{a_n}}=2{a_1}$,
∴am•an=4${{a}_{1}}^{2}$=${{a}_{2}}^{2}$,
∴m+n=4,
∴$\frac{1}{m}+\frac{4}{n}$=$\frac{1}{4}$($\frac{1}{m}+\frac{4}{n}$)(m+n)=$\frac{1}{4}$+1+$\frac{n}{4m}$+$\frac{m}{n}$≥$\frac{5}{4}$+2$\sqrt{\frac{n}{4m}•\frac{m}{n}}$=$\frac{9}{4}$,当且仅当$\frac{n}{4m}=\frac{m}{n}$,并且m+n=4时取等号.
故选:D.
点评 本题主要考查等比数列的运算性质以及基本不等式的应用,涉及的知识点较多,要求熟练掌握基本不等式成立的条件.

练习册系列答案
相关题目
2.若复数z满足(1+i)z=2i,其中i为虚数单位,则$\overline z$( )
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
6.执行如图的程序框图,则输出x的值是( )
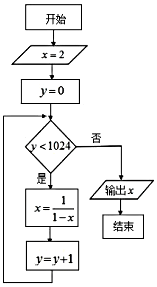

| A. | 2016 | B. | 1024 | C. | $\frac{1}{2}$ | D. | -1 |