题目内容

在△ABC中，角A、B、C所对的边分别为a、b、c，若a=5，b=4，cosA=cos2B，则c的值是
 
．
考点：余弦定理的应用
专题：解三角形
分析：利用正弦定理，通过平方关系求出A的余弦函数值，然后通过余弦定理求出c的大小．
解答： 解：在△ABC中，角A、B、C所对的边分别为a、b、c，若a=5，b=4，
由
a
sinA
=
b
sinB
，可得5sinB=4sinA，
可得25sin2B=16sin2A，即25-25cos2B=16-16cos2A，
∵cosA=cos2B，代入上式，
∴16cos2A-25cosA+9=0，
解得cosA=
9
16
，或cosA=1（舍去）．
由余弦定理可得，2bccosA=b2+c2-a2，
2×4•c×
9
16
=16+c2-25，
可得2c2-9c-18=0，
解得c=6．
故答案为：6．
点评：本题考查余弦定理的应用以及正弦定理的应用，考查计算能力以及转化思想．
练习册系列答案
相关题目
已知Sn是等比数列{an}的前n项和，S3，S9，S6成等差数列．
（Ⅰ）求数列{an}的公比q；
（Ⅱ）证明：ak，ak+6，ak+3（k∈N*）成等差数列．
若m-
1
2
＜x≤m+
1
2
（其中m为整数），则称m为离实数x最近的整数，记作I[x]，即I[x]=m．设集合A={（x，y）|f（x）=x-I[x]，x∈R}，B={（x，y）|g（x）=logax}，其中0＜a＜1，若集合A∩B的元素恰有三个，则a的取值范围为
 
．
执行如图所示的程序框图，则输出的T值为
 
．
已知复数z满足|z-2-3i|=1，则|z+1+i|的最小值为
 
．
一个空间几何体的三视图如图所示，该几何体的表面积为
 
．
已知偶函数f（x）是定义在R上的函数，对x∈R都有f（x+6）=f（x）+f（3），若当x∈（-3，-2）时，f（x）=5x，则f（201.5）=
 
．
设数列{an}是由集合{3s+3t|0≤s＜t，且s，t∈Z}中所有的数从小到大排列成的数列，即a1=4，a2=10，a3=12，a4=28，a5=30，a6=36，…，若a2013=3m+3n（0≤m＜n，且m，n∈Z}，则m+n的值等于
 
．
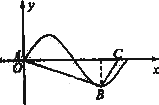已知函数f（x）=sinωx（ω＞0）的一段图象如图所示，△ABC的顶点A与坐标原点O重合，B是f（x）的图象上一个最低点，C在x轴上，若内角A，B，C所对边长为a，b，c，且△ABC的面积S满足12S=b2+c2-a2，将f（x）右移一个单位得到g（x），则g（x）的表达式为（　　）
A、g（x）=cos（
π
2
x）
B、g（x）=-cos（
π
2
x）
C、g（x）=sin（
x
2
+
1
2
）
D、g（x）=sin（
x
2
-
1
2
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网