题目内容
1.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线x2-y2=1相交于A,B两点,若△ABF为等边三角形,则p=$2\sqrt{3}$.分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形求出p即可.
解答 解:抛物线的焦点坐标为(0,$\frac{P}{2}$),准线方程为:y=-$\frac{P}{2}$,
准线方程与双曲线x2-y2=1联立可得:x2-($-\frac{P}{2}$)2=1,
解得x=±$\sqrt{1+\frac{{P}^{2}}{4}}$,
因为△ABF为等边三角形,所以$\sqrt{{x}^{2}+{p}^{2}}$=2|x|,即p2=3x2,
即p2=3($1+\frac{{P}^{2}}{4}$),解得p=2$\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
11.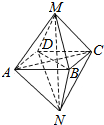 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )
 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )| A. | 该几何体是由两个同底的四棱锥组成的几何体 | |
| B. | 该几何体有12条棱、6个顶点 | |
| C. | 该几何体有8个面,并且各面均为三角形 | |
| D. | 该几何体有9个面,其中一个面是四边形,其余均为三角形 |
11.当x→0时,下列4个无穷小量中比其它3个更高阶的无穷小量是( )
| A. | 1n(1+x) | B. | ex-1 | C. | tanx-sinx | D. | 1-cosx |