题目内容
(
+
)n展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:由于(
+
)n展开式中只有第六项的二项式系数最大,故n=10,
故(
+
)10展开式的通项公式为 Tr+1=
•2r•x5-
,令5-
=0,求得 r=2,
∴展开式中的常数项是
•22=180,
故选:A.
| x |
| 2 |
| x2 |
故(
| x |
| 2 |
| x2 |
| C | r 10 |
| 5r |
| 2 |
| 5r |
| 2 |
∴展开式中的常数项是
| C | 2 10 |
故选:A.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
双曲线
-
=1({a>0,b>0})的渐近线为y=±
x,其顶点到渐近线的距离为1,则双曲线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在长方形ABCD中,AB=2,AD=1,则
•
=( )
| AC |
| CD |
| A、-2 | B、2 | C、4 | D、-4 |
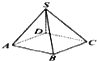 如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )| A、60 | B、480 |
| C、420 | D、70 |
函数f(x)是定义域为R的偶函数,当x>0时f(x)=-x+1,则当x<0时,f(x)的表达式为( )
| A、f(x)=-x+1 |
| B、f(x)=-x-1 |
| C、f(x)=x+1 |
| D、f(x)=x-1 |
对于实数对(a,b)和(c,d),规定:(a,b)=(c,d)当且仅当a=c,c=d,定义运算如下:
①(a,b)?(c,d)=(ac-bd,bc+ad);
②(a,b)⊕(c,d)=(a+c,b+d).
设p,q∈R,若(1,2)?(p,q)=(5,0),则(1,2)⊕(p,q)等于( )
①(a,b)?(c,d)=(ac-bd,bc+ad);
②(a,b)⊕(c,d)=(a+c,b+d).
设p,q∈R,若(1,2)?(p,q)=(5,0),则(1,2)⊕(p,q)等于( )
| A、(4,0) |
| B、(2,0) |
| C、(0,2) |
| D、(0,4) |
函数f(x)是定义在区间[-5,5]上的偶函数,且在[0,5]上是单调函数,f(1)<f(3),则下列各式一定成立的是( )
| A、f(0)>f(5) |
| B、f(3)<f(2) |
| C、f(-1)>f(3) |
| D、f(-2)>f(1) |