题目内容
在长方形ABCD中，AB=2，AD=1，则
•
=（ ）
| AC |
| CD |
| A、-2 | B、2 | C、4 | D、-4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的垂直与数量积的关系、向量的三角形法则、数量积运算即可得出．
解答：
解：∵
⊥
，∴
•
=0．
∵
=
+
，
=-
，
∴
•
=(
+
)•(-
)
=-
2-0
=-22=-4．
故选：D．
| AD |
| AB |
| AD |
| AB |
∵
| AC |
| AB |
| AD |
| CD |
| AB |
∴
| AC |
| CD |
| AB |
| AD |
| AB |
=-
| AB |
=-22=-4．
故选：D．
点评：本题考查了向量的垂直与数量积的关系、向量的三角形法则、数量积运算，属于基础题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
计算定积分
（x2+sinx）dx=（ ）
| ∫ | 1 -1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若点P（sin2，cos2）是角α终边上一点，则角α终边所在象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知等比数列{an}的公比为正数，且a5=2a3，a2=2，则a1=（ ）
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
设函数在R上的导函数为f′（x），且f（x）+xf′（x）＞0，下面的不等式在R上恒成立的是（ ）
| A、f（x）＞0 |
| B、f（x）＜0 |
| C、f（x）＞x |
| D、f（x）＜x |
（
+
）n展开式中只有第六项的二项式系数最大，则展开式中的常数项是（ ）
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
对于实数对（a，b）和（c，d），规定：（a，b）=（c，d）当且仅当a=c，c=d定义运算如下：
①（a，b）?（c，d）=（ac-bd，bc+ad）；
②（a，b）⊕（c，d）=（a+c，b+d）．
设p，q∈R，若（1，2）?（p，q）=（5，0），则（1，2）⊕（p，q）等于（ ）
①（a，b）?（c，d）=（ac-bd，bc+ad）；
②（a，b）⊕（c，d）=（a+c，b+d）．
设p，q∈R，若（1，2）?（p，q）=（5，0），则（1，2）⊕（p，q）等于（ ）
| A、（4，0） |
| B、（2，0） |
| C、（0，2） |
| D、（0，2） |
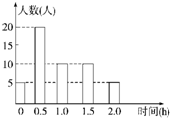某校为了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天课外阅读所用时间的数据，结果用条形图表示如下．根据条形图可得这50名学生这一天平均每人的课外阅读时间为（ ）| A、0.6 h |
| B、0.9 h |
| C、1.0 h |
| D、1.5 h |