题目内容
设x为实数,求证:1+2x4≥x2+2x3.
考点:不等式的证明
专题:证明题
分析:将所证的不等式作差后化积,通过判断符号即可证得结论成立.
解答:
证明:∵x为实数,
∴1+2x4-x2-2x3
=2x3(x-1)-(x-1)(x+1)
=(x-1)(2x3-x-1)
=(x-1)[(x-1)(2x2+2x+1)]
=(x-1)2[2(x+
)2+
]≥0,
∴1+2x4≥x2+2x3.
∴1+2x4-x2-2x3
=2x3(x-1)-(x-1)(x+1)
=(x-1)(2x3-x-1)
=(x-1)[(x-1)(2x2+2x+1)]
=(x-1)2[2(x+
| 1 |
| 2 |
| 1 |
| 2 |
∴1+2x4≥x2+2x3.
点评:本题考查不等式的证明,着重考查作差法的应用,作差后化积是关键,考查运算能力,属于中档题.

练习册系列答案
相关题目
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,an,输出A,B,则( )
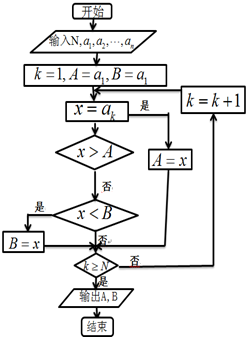

| A、A和B分别是a1,a2,…,an中最小的数和最大的数 | ||
| B、A和B分别是a1,a2,…,an中最大的数和最小的数 | ||
C、
| ||
| D、A+B为a1,a2,…,an的和 |
 如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=2AB,SA=SD,SA⊥AB,N是棱AD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=2AB,SA=SD,SA⊥AB,N是棱AD的中点.