题目内容
15.已知函数f(x)=ax-lnx.(1)过原点O作函数f(x)图象的切线,求切点的横坐标;
(2)对?x∈[1,+∞),不等式f(x)≥a(2x-x2)恒成立,求实数a的取值范围.
分析 (1)通过设切点坐标,进而可写出切线方程,代入原点计算即得结论;
(2)通过转化可知a(x2-x)≥lnx对?x∈[1,+∞)恒成立,分别设y1=a(x2-x),y2=lnx,利用x∈[1,+∞)可知a>0.再记g(x)=ax2-ax-lnx,通过举反例可知当0<a<1时不满足题意.进而转化为函数的最值问题,利用当x>1时lnx<x-1恒成立放缩即得结论.
解答 解:(1)设切点为M(x0,f(x0)),直线的切线方程为y-f(x0)=k(x-x0),
∵f′(x)=a-$\frac{1}{x}$,∴k=f′(x0)=a-$\frac{1}{{x}_{0}}$,
即直线的切线方程为y-ax0+lnx0=(a-$\frac{1}{{x}_{0}}$)(x-x0),
又切线过原点O,所以-ax0+lnx0=-ax0+1,
由lnx0=1,解得x0=e,所以切点的横坐标为e.
(2)∵不等式ax-lnx≥a(2x-x2)恒成立,
∴等价于a(x2-x)≥lnx对?x∈[1,+∞)恒成立.
设y1=a(x2-x),y2=lnx,由于x∈[1,+∞),且当a≤0时y1≤y2,故a>0.
记g(x)=ax2-ax-lnx,
则当0<a<1时,g(3)=6a-ln3≥0不恒成立,同理x取其他值不恒成立.
当x=1时,g(x)≥0恒成立;
当x>1时,则a≥$\frac{lnx}{{x}^{2}-x}$恒成立,等价于问题转化为求h(x)=$\frac{lnx}{{x}^{2}-x}$当x>1时的最大值.
又当x>1时,lnx<x-1<x(x-1),即h(x)=$\frac{lnx}{{x}^{2}-x}$<1(x>1),
综上所述:a≥1.
点评 本题是一道关于导数的综合题,考查转化与化归思想,注意解题方法的积累,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案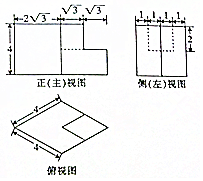
| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |
| 137 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
| 431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
| A. | 0.40 | B. | 0.30 | C. | 0.35 | D. | 0.25 |