题目内容
12.已知关于x的不等式$\frac{lo{g}_{a}x}{lnx}$-$\frac{4}{lnx}$<lnx(a>0且a≠1)对任意的x∈(1,100)恒成立,则实数a的取值范围为(0,1)∪(${e}^{\frac{1}{4}}$,+∞).分析 问题转化为$\frac{1}{lna}$<lnx+$\frac{4}{lnx}$,x∈(1,100),令h(x)=lnx+$\frac{4}{lnx}$,x∈(1,100),求出h(x)的值域,从而求出a的范围即可.
解答 解:∵$\frac{lo{g}_{a}x}{lnx}$-$\frac{4}{lnx}$<lnx,
∴$\frac{1}{lna}$<lnx+$\frac{4}{lnx}$,x∈(1,100),
令h(x)=lnx+$\frac{4}{lnx}$,x∈(1,100),
则lnx>0,
故h(x)≥2$\sqrt{lnx•\frac{4}{lnx}}$=4,
当且仅当lnx=2时“=”成立,
而h(100)=2ln10+$\frac{2}{ln10}$,
而x→1时,lnx→0,h(x)→+∞,
故h(x)∈[4,+∞),
故$\frac{1}{lna}$<4,
0<a<1时,lna<0,成立,
a>1时,lna>0,
只需lna>$\frac{1}{4}$,即a>${e}^{\frac{1}{4}}$即可,
综上:a∈(0,1)∪(${e}^{\frac{1}{4}}$,+∞),
故答案为:(0,1)∪(${e}^{\frac{1}{4}}$,+∞).
点评 本题考查了函数的单调性、最值问题,考查不等式的性质,是一道中档题.

练习册系列答案
相关题目
2.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
20.已知一个几何体的三视图如图所示,则该几何体的表面积为( )
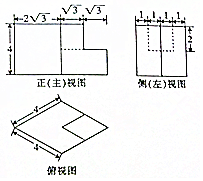

| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |
17.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1,则( )
| A. | $f(6)<f(-7)<f(\frac{11}{2})$ | B. | $f(6)<f(\frac{11}{2})<f(-7)$ | C. | $f(-7)<f(\frac{11}{2})<f(6)$ | D. | $f(\frac{11}{2})<f(-7)<f(6)$ |