题目内容
已知等差数列{an}满足an+an+1=n+
.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn;
(3)若a1,am,a3m成等比数列,求m的值.
| 1 |
| 2 |
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn;
(3)若a1,am,a3m成等比数列,求m的值.
考点:等比数列的性质,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)解法一:利用基本量法,求出首项与公差,即可求{an}的通项公式;解法二:求出an+an+1=2a1+(2n-1)•d=2dn+2a1-d,所以有2dn+2a1-d=n+
对n∈N*成立,求出首项与公差,即可求{an}的通项公式;
(2)利用等差数列的求和公式,可求{an}的前n项和Sn;
(3)若a1,am,a3m成等比数列,利用等比数列的性质,即可求m的值.
| 1 |
| 2 |
(2)利用等差数列的求和公式,可求{an}的前n项和Sn;
(3)若a1,am,a3m成等比数列,利用等比数列的性质,即可求m的值.
解答:
解:(1)解法一:设{an}的公差为d,因为an+an+1=n+
,
所以有
,两式相减得到,2d=1,即d=
….(2分)
代入得到a1=
….(4分)
所以an=
+(n-1)•
=
….(6分)
解法二:设{an}的公差为d,
则an=a1+(n-1)•d,an+1=a1+n•d,….(2分)
所以an+an+1=2a1+(2n-1)•d=2dn+2a1-d
所以有2dn+2a1-d=n+
对n∈N*成立,
所以有
,解得
….(4分)
所以an=
+(n-1)•
=
….(6分)
(2)因为Sn=
n,所以Sn=
….(9分)
(3)因为a1,am,a3m成等比数列,所以(am)2=a1a3m….(10分)
即
=
•
….(11分)
解得m=3,m=0(舍掉)
所以m=3….(12分)
| 1 |
| 2 |
所以有
|
| 1 |
| 2 |
代入得到a1=
| 1 |
| 2 |
所以an=
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
解法二:设{an}的公差为d,
则an=a1+(n-1)•d,an+1=a1+n•d,….(2分)
所以an+an+1=2a1+(2n-1)•d=2dn+2a1-d
所以有2dn+2a1-d=n+
| 1 |
| 2 |
所以有
|
|
所以an=
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
(2)因为Sn=
| (a1+an) |
| 2 |
| (n+1)n |
| 4 |
(3)因为a1,am,a3m成等比数列,所以(am)2=a1a3m….(10分)
即
| m2 |
| 4 |
| 1 |
| 2 |
| 3m |
| 2 |
解得m=3,m=0(舍掉)
所以m=3….(12分)
点评:本题考查等差数列的通项与求和,考查等比数列的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
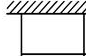 如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.
如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.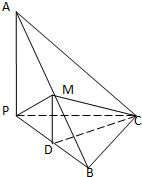 如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.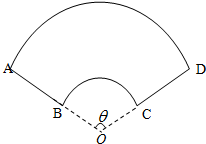 某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.