题目内容
6.在△ABC中,已知a=17,b=24,A=45°,则此三角形( )| A. | 无解 | B. | 有两解 | C. | 有一解 | D. | 解的个数不确定 |
分析 由题意求出a边上的高h,画出图象后,结合条件判断出此三角形解的情况.
解答 解:由题意知,a=17,b=24,A=45°
则c边上的高h=bsinA=$24×\frac{\sqrt{2}}{2}$=12$\sqrt{2}$,
如右图所示:
因12$\sqrt{2}$<a=17<b,
所以此三角形有两解,
故选B.
点评 本题考查了三角形解的情况,以及数形结合思想.

练习册系列答案
相关题目
14.高考后,4位考生各自在甲、乙两所大学中任选一所参观,则甲、乙两所大学都有考生参观的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
1.如图,四边形ABCD是圆柱的轴截面,E是底面圆周上异于A、B的一点,则下面结论中错误的是( )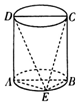

| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
8.若对于定义在R上的函数f(x)当且仅当存在有限个非零自变量x,使得f(-x)=f(x),则称f(x)为类偶函数,若函数f(x)=x3+(a2-2a)x+a为类偶函数,则f(a)的取值范围为( )
| A. | (0,2) | B. | (-∞,0]∪[2,+∞) | C. | [0,2] | D. | (-∞,0]∪(2,+∞) |
