题目内容
9.在平面直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}x=cosφ\\ y=sinφ\end{array}$(φ为参数),曲线C2的参数方程为$\left\{\begin{array}{l}x=acosφ\\ y=bsinφ\end{array}$(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点,当α=0时,这两个交点间的距离为2,当α=$\frac{π}{2}$时,这两个交点重合.(Ⅰ)分别说明C1,C2是什么曲线,并求a与b的值;
(Ⅱ)设当α=$\frac{π}{4}$时,l与C1,C2的交点分别为A1,B1,当α=-$\frac{π}{4}$时,l与C1,C2的交点分别为A2,B2,求直线A1 A2、B1B2的极坐标方程.
分析 (Ⅰ) 曲线C1的直角坐标方程为x2+y2=1,C1是以(0,0)为圆心,以1为半径的圆,曲线C2的直角坐标方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,C2是焦点在x轴上的椭圆.当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),当$α=\frac{π}{2}$时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),由此能求出a,b.
(Ⅱ) C1,C2的普通方程分别为x2+y2=1和$\frac{x^2}{9}+{y^2}=1$,当$α=\frac{π}{4}$时,射线l与C1的交点A1的横坐标为$x=\frac{{\sqrt{2}}}{2}$,与C2的交点B1的横坐标为$x'=\frac{{3\sqrt{10}}}{10}$,当$α=-\frac{π}{4}$时,射线l与C1,C2的交点A2,分别与A1,B1关于x轴对称,由此能求出直线A1 A2 和B1B2的极坐标方程.
解答 (本题满分10分)【选修4-4 坐标系统与参数方程】
解:(Ⅰ)∵曲线C1的参数方程为$\left\{\begin{array}{l}x=cosφ\\ y=sinφ\end{array}$(φ为参数),
∴曲线C1的直角坐标方程为x2+y2=1,∴C1是以(0,0)为圆心,以1为半径的圆,
∵曲线C2的参数方程为$\left\{\begin{array}{l}x=acosφ\\ y=bsinφ\end{array}$(a>b>0,φ为参数),
∴曲线C2的直角坐标方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,∴C2是焦点在x轴上的椭圆.
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),
∵这两点间的距离为2,∴a=3…(2分)
当$α=\frac{π}{2}$时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),
∵这两点重合,∴b=1…(5分)
(Ⅱ) C1,C2的普通方程分别为x2+y2=1和$\frac{x^2}{9}+{y^2}=1$…(6分)
当$α=\frac{π}{4}$时,解方程组$\left\{\begin{array}{l}{y=x}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,得A1($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),即射线l与C1的交点A1的横坐标为$x=\frac{{\sqrt{2}}}{2}$,
解方程组$\left\{\begin{array}{l}{y=x}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,得B1($\frac{3\sqrt{10}}{10}$,$\frac{3\sqrt{10}}{10}$),与C2的交点B1的横坐标为$x'=\frac{{3\sqrt{10}}}{10}$
当$α=-\frac{π}{4}$时,射线l与C1,C2的交点A2,分别与A1,B1关于x轴对称
因此,直线A1 A2、B1B2垂直于极轴,
故直线A1 A2 和B1B2的极坐标方程分别为$ρcosθ=\frac{{\sqrt{2}}}{2}$,$ρcosθ=\frac{{3\sqrt{10}}}{10}$…(10分)
点评 本题考查图形的判断与实数值的求法,考查极坐标方程的求法,是中档题,解题时要认真审题,注意参数方程、直角坐标方程、极坐标方程间相互转化公式的合理运用.

| X | -1 | 0 | 1 |
P | $\frac{1}{2}$ | $1-\frac{3}{2}q$ | q2 |
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{17}{16}$ | D. | $\frac{11}{16}$ |
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
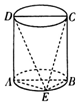
| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
| A. | (0,2) | B. | (-∞,0]∪[2,+∞) | C. | [0,2] | D. | (-∞,0]∪(2,+∞) |
| A. | i | B. | 1+i | C. | -i | D. | 1-i |
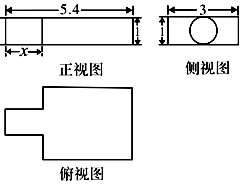 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.