题目内容
13.已知长方体ABCD-A1B1C1D1的外接球O的体积为$\frac{32π}{3}$,其中BB1=2,则三棱锥O-ABC的体积的最大值为( )| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
分析 设AB=a,AD=b,推导出a2+b2=12,ab≤$\frac{{a}^{2}+{b}^{2}}{2}$=6,由此能求出三棱锥O-ABC的体积的最大值.
解答 解:设AB=a,AD=b,
∵长方体ABCD-A1B1C1D1的外接球O的体积为$\frac{32π}{3}$,BB1=2,
∴外接球O的半径R=2,
∴a2+b2+4=16,
∴a2+b2=12,
∴ab≤$\frac{{a}^{2}+{b}^{2}}{2}$=6,
∵O到平面ABC的距离d=$\frac{1}{2}$BB1=1,
S△ABC=$\frac{1}{2}ab$≤3,
∴三棱锥O-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×d$≤$\frac{1}{3}×3×1$=1.
∴三棱锥O-ABC的体积的最大值为1.
故选:A.
点评 本题考查三棱锥的体积的最大值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
3.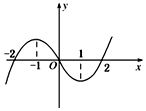 在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )
在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )
 在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )
在R上可导的函数f(x)的图象如图示,f′(x)为函数f(x)的导数,则关于x的不等式x•f′(x)<0的解集为( )| A. | (-∞,-1)∪(0,1) | B. | (-2,-1)∪(1,2) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-2)∪(2,+∞) |
1.已知等比数列{an}共有10项,其中奇数项之积为2,偶数项之积为64,则其公比是( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
18.若$tanα=3tan\frac{π}{7}$,则$\frac{{cos({α-\frac{5π}{14}})}}{{sin({α-\frac{π}{7}})}}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知cos$\frac{4π}{5}cos\frac{7π}{15}-sin\frac{9π}{5}$sin$\frac{7π}{15}$=cos(x+$\frac{π}{2}$)cosx+$\frac{2}{3}$,则sin2x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
2.下列几何体的截面图不可能是四边形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 圆台 | D. | 棱台 |
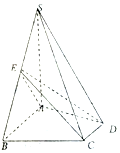 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.