下列几何体的截面图不可能是四边形的是( )A．圆柱B．圆锥C．圆台D．棱台题目和参考答案——青夏教育精英家教网—

题目内容

2．下列几何体的截面图不可能是四边形的是（　　）

A．

圆柱

B．

圆锥

C．

圆台

D．

棱台

分析在A中，圆柱的纵切面是四边形；在B中，圆锥的纵切面是三角形，横切面是圆；在C中，圆台的纵切面是四边形；在D中，四棱台的截面图可能是四边形．

解答解：在A中，圆柱的纵切面是四边形，故A不正确；
在B中，圆锥的纵切面是三角形，横切面是圆，
∴圆锥的截面图不可能是四边形，故B正确；
在C中，圆台的纵切面是四边形，故C不正确；
在D中，四棱台的截面图可能是四边形，故D不正确．
故选：B．

点评本题考查圆柱、圆锥、圆台、棱台的结构特征的应用，是基础题，解题时要认真审题，注意基本概念的熟练掌握．

练习册系列答案

相关题目

12．

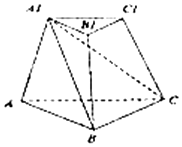如图，在三棱台ABC-A₁B₁C₁中，截去三棱锥A₁-ABC，则剩余部分是（　　）

13．已知长方体ABCD-A₁B₁C₁D₁的外接球O的体积为$\frac{32π}{3}$，其中BB₁=2，则三棱锥O-ABC的体积的最大值为（　　）

10．已知命题p：对任意x∈R，有cosx≤1，则（　　）

	A．	￢p：存在x∈R，使cosx＞1		B．	￢p：对任意x∈R，有cosx＞1
	C．	￢p：存在x∈R，使cosx≥1		D．	￢p：对任意x∈R，有cosx≥1

17．已知曲线y=$\frac{x^2}{4}$-lnx的一条切线的斜率为$\frac{1}{2}$，则切点的横坐标为（　　）

7．过点（2，1）作圆（x-1）²+（y+2）²=25的弦，其中最短的弦所在的直线方程为（　　）

14．已知函数f（x）=x²-cosx，对于$[-\frac{π}{2}，\frac{π}{2}]$上的任意x₁，x₂，有如下条件：
①x₁＞x₂；②x₁²＞x₂²；③|x₁|＞x₂；④x₁+x₂＜0；⑤x₁＞|x₂|．
其中能使f（x₁）＞f（x₂）恒成立的条件序号是②．

11．

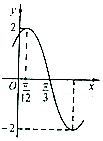已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0）f（x）=Asin（ωx+φ）的部分图象如图所示，下列说法正确的是（　　）

	A．	函数f（x）的最小正周期为2π
	B．	函数f（x）的图象关于点$（{-\frac{5π}{12}，0}）$对称
	C．	将函数f（x）的图象向左平移$\frac{π}{6}$个单位得到的函数图象关于y轴对称
	D．	函数f（x）的单调递增区间是$[{kπ+\frac{7π}{12}，kπ+\frac{13π}{12}}]，k∈Z$

12．已知直线xcosθ-y+2=0，（θ∈R）的倾斜角为α，则α的取值范围为$[0，\frac{π}{4}]∪[\frac{3π}{4}，π）$．

试题分类