题目内容
19.已知f(x)=$\sqrt{3}$cos2x-sinxcosx(I)求函数f(x)的最大值及对应x的值;
(Ⅱ)在△ABC中,∠A,∠B,∠C所对的边分别是a、b、c,若($\frac{C}{2}$,$\frac{\sqrt{3}}{2}$)是函数f(x)图象的一个对称中心,且△ABC的周长为6时,求△ABC面积的最大值.
分析 (1)依次利用余弦降幂、正弦倍角,辅助角公式化简函数f(x),得到最简形式.
(2)从正弦函数的图象可以分析得到图象的对称中心在正弦函数图象上,故带入函数即可得到C角的值,再利用余弦定理与基本不等式求出ab,从而得到三角形面积的最值.
解答 解:(1)∵f(x)=$\sqrt{3}$cos2x-sinxcosx,
由三角恒等式:2cos2x=1+cos2x,及sin2x=2sinxcosx,
∴f(x)=$\frac{\sqrt{3}(1+cos2x)}{2}$-$\frac{sin2x}{2}$=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}cos2x-sin2x}{2}$,
由辅助角公式得f(x)=$\frac{\sqrt{3}}{2}$-sin(2x-$\frac{π}{3}$),
∴f(x)max=$\frac{\sqrt{3}}{2}$+1,
此时x=-$\frac{π}{12}$+kπ(k∈Z),
(2)∵f(x)=$\frac{\sqrt{3}}{2}$-sin(2x-$\frac{π}{3}$),
∵($\frac{C}{2}$,$\frac{\sqrt{3}}{2}$)是函数f(x)图象的一个对称中心,
∴sin(C-$\frac{π}{3}$)=0,
得:C=$\frac{π}{3}$,
△ABC的面积S=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab,
由余弦定理知cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∴12+ab=4(a+b),
由基本不等式得:12+ab≥8$\sqrt{ab}$,
∴($\sqrt{ab}$-2)($\sqrt{ab}$-6)≥0,
∴ab≤4或ab≥36(舍),
∴当ab=4时,面积最大,为$\sqrt{3}$,
此时a=b=c=2.
点评 本题考查余弦降幂、正弦倍角,辅助角公式,需熟练掌握.将对称中心带入函数即可得到C角的值,再利用余弦定理与基本不等式求出ab,从而得到三角形面积的最值.

| A. | x2-2x+1>0 | B. | |x-1|>0 | C. | 2x+1>0 | D. | log2(x2+1)>0 |
| A. | [-$\frac{4}{3}$,$\frac{4}{3}$] | B. | [-$\frac{4}{3}$,0] | C. | [0,$\frac{4}{3}$] | D. | [0,1] |
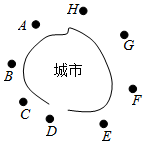 某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.
某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.