题目内容
10.函数f(x)=$\frac{\sqrt{1-{x}^{2}}-1}{x-2}$的值域是( )| A. | [-$\frac{4}{3}$,$\frac{4}{3}$] | B. | [-$\frac{4}{3}$,0] | C. | [0,$\frac{4}{3}$] | D. | [0,1] |
分析 先求出函数的定义域,利用换元法转化为两点间的斜率关系,利用数形结合进行求解即可.
解答 解:由$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{x-2≠0}\end{array}\right.$得$\left\{\begin{array}{l}{-1≤x≤1}\\{x≠2}\end{array}\right.$,则-1≤x≤1,即函数的定义域为[-1,1],
设x=sinα,则函数f(x)等价为y=$\frac{\sqrt{1-si{n}^{2}α}-1}{sinα-2}$=$\frac{|cosα|-1}{sinα-2}$,
设P(sinα,|cosα|),则点P在单位圆x2+y2=1的上半部分,
则$\frac{|cosα|-1}{sinα-2}$的几何意义是圆上点到点A(2,1)的斜率,
由图象知AB的斜率最小,此时k=0,
AC的斜率最大,此时k=$\frac{0-1}{1-2}=\frac{-1}{-1}$=1,
故0≤k≤1,
故函数f(x)的值域是[0,1],
故选:D
点评 本题主要考查函数值域的求解,利用换元法转化为两点斜率的关系是解决本题的关键.综合性较强.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
18.地球上,在北纬30°圈上有两个点A、B,它们的经度之差为180°,则A、B两点间的球面距离为(地球的半径为R)( )
| A. | $\frac{\sqrt{3}}{3}$R | B. | $\frac{1}{3}$πR | C. | $\frac{1}{2}$πR | D. | $\frac{2}{3}$πR |
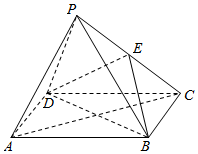 如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.
如图,四棱锥P-ABCD中,底面ABCD是边长等于2的正方形,其他四个侧面都是边长等于$\sqrt{5}$的等腰三角形,点E是PC中点.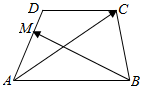 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.