题目内容
14.用“五点法”画函数y=1-sin3x,x∈[$\frac{π}{3}$,$\frac{5π}{3}$]的图象,是否能求该函数图象与直线x=$\frac{π}{3}$,x=$\frac{5π}{3}$及x轴所围成的图象的面积?分析 根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图;结合积分的应用求出区域的面积.
解答 解(1):函数的周期T=$\frac{2π}{3}$先作出函数在一个周期内的图象,然后利用平移法得到在[$\frac{π}{3}$,$\frac{5π}{3}$]内的图象:
| 3x | π | $\frac{3π}{2}$ | 2π | $\frac{5π}{2}$ | 3π |
| x | $\frac{π}{3}$ | $\frac{π}{2}$ | $\frac{2π}{3}$ | $\frac{5π}{6}$ | π |
| y | 1 | 2 | 1 | 0 | 1 |
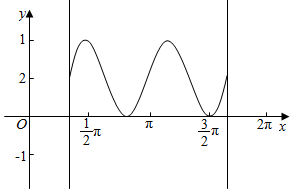
则函数图象与直线x=$\frac{π}{3}$,x=$\frac{5π}{3}$及x轴所围成的图象的面积S=∫${\;}_{\frac{π}{3}}^{\frac{5π}{3}}$(1-sin3x)dx=(x+$\frac{1}{3}$cos3x)|${\;}_{\frac{π}{3}}^{\frac{5π}{3}}$
=$\frac{5π}{3}$+$\frac{1}{3}$cos(3×$\frac{5π}{3}$)-$\frac{π}{3}$+$\frac{1}{3}$cos(3×$\frac{π}{3}$)=$\frac{5π}{3}$-$\frac{1}{3}$-$\frac{π}{3}$-$\frac{1}{3}$=$\frac{4π}{3}$-$\frac{2}{3}$.
点评 本题主要考查三角函数的图象和性质,以及利用积分法求区域面积,要求熟练掌握五点法作图以及函数图象之间的变化关系.

练习册系列答案
相关题目
4.圆x2+y2-8x+6y+16=0与圆x2+y2=64的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 相离 | D. | 外切 |
9.过抛物线C:y2=2px(p>0)的焦点F且倾斜角为45°的直线交C于A,B两点,若以AB为直径的圆被x轴截得的弦长为16$\sqrt{3}$,则p的值为( )
| A. | 8 | B. | 8$\sqrt{3}$ | C. | 12 | D. | 16 |
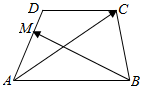 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.