题目内容
已知函数f（x）=
（Ⅰ）分别求f（2）+f（
），f（3）+f（
），f（4）+f（
） 的值；
（Ⅱ）归纳猜想一般性结论，并给出证明；
（Ⅲ）求值：2f（2）+2f（3）+…+2f（2014）+f（
）+f（
）+…+f（
）+
f（2）+
f（3）+…+
f（2014）．
| x2 |
| 1+x2 |
（Ⅰ）分别求f（2）+f（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
（Ⅱ）归纳猜想一般性结论，并给出证明；
（Ⅲ）求值：2f（2）+2f（3）+…+2f（2014）+f（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20142 |
考点：函数的值
专题：综合题,函数的性质及应用
分析：（Ⅰ）代入解析式可分别求得结果；
（Ⅱ）由（Ⅰ）猜想f（x）+f（
）=1，代入解析式可证明；
（Ⅲ）可得f（x）+
f（x）=
(1+
)=1，再由（Ⅱ）得f（x）+f（
）=1，对目标式分组求和即可；
（Ⅱ）由（Ⅰ）猜想f（x）+f（
| 1 |
| x |
（Ⅲ）可得f（x）+
| 1 |
| x2 |
| x2 |
| 1+x2 |
| 1 |
| x2 |
| 1 |
| x |
解答：
解：（Ⅰ）∵f（x）=
，
∴f（2）+f（
）=
+
=
+
=1，
同理可得f（3）+f（
）=1，f（4）+f（
）=1．
（Ⅱ）由（Ⅰ）猜想f（x）+f（
）=1，
证明：f（x）+f（
）=
+
=
+
=1．
（Ⅲ）∵f（x）+
f（x）=
(1+
)=1，由（Ⅱ）得f（x）+f（
）=1，
则2f（2）+2f（3）+…+2f（2014）+f（
）+f（
）+…+f（
）+
f（2）+
f（3）+…+
f（2014）
=[f（2）+f（
）+f（2）+
f(2)]+[f（3）+f（
）+
f(3)]+[f（2014+f（
）+f（2014）+
f(2014)]
=
=4026．
| x2 |
| 1+x2 |
∴f（2）+f（
| 1 |
| 2 |
| 22 |
| 1+22 |
(
| ||
1+(
|
| 22 |
| 1+22 |
| 1 |
| 1+22 |
同理可得f（3）+f（
| 1 |
| 3 |
| 1 |
| 4 |
（Ⅱ）由（Ⅰ）猜想f（x）+f（
| 1 |
| x |
证明：f（x）+f（
| 1 |
| x |
| x2 |
| 1+x2 |
(
| ||
1+(
|
| x2 |
| 1+x2 |
| 1 |
| 1+x2 |
（Ⅲ）∵f（x）+
| 1 |
| x2 |
| x2 |
| 1+x2 |
| 1 |
| x2 |
| 1 |
| x |
则2f（2）+2f（3）+…+2f（2014）+f（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20142 |
=[f（2）+f（
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 2014 |
| 1 |
| 20142 |
=
| ||
| 2013个2 |
点评：该题考查函数的性质、函数值的求解，考查学生的运算求解能力，属中档题．
练习册系列答案
相关题目
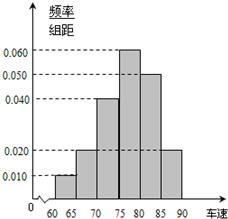某调查公司在某服务区调查七座以下小型汽车在某段高速公路的车速（km/t），办法是按汽车进服务区的先后每间隔50辆抽取一辆的抽样方法抽取40名驾驶员进行询问，将调查结果按[60，65）[65，70）[70，75）[75，80），[80，85）[85，90）分成六段，并得到如图所示的频率分布直方图．