题目内容
函数y=esinx(-π≤x≤π)(e=2.71828…)的大致图象为( )
A、 |
B、 |
C、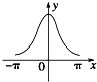 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:故令t=sinx,原函数等价于函数f(t)=et,由于当x=
时,et取最大值e1=e,故原函数当x=
时取最大值e,从而可知D正确.
| π |
| 2 |
| π |
| 2 |
解答:
解:由于f(x)=esinx,
故令t=sinx,∴原函数等价于函数f(t)=et,
∵-π≤x≤π,∴当x=
时,t取最大值1,
∴当x=
时,et取最大值e1=e,
∴当x=
时,函数y=esinx取最大值e,
故4个选项中只有D符合,
故选:D.
故令t=sinx,∴原函数等价于函数f(t)=et,
∵-π≤x≤π,∴当x=
| π |
| 2 |
∴当x=
| π |
| 2 |
∴当x=
| π |
| 2 |
故4个选项中只有D符合,
故选:D.
点评:本题考查复合函数的性质,考查同学们对函数基础知识的把握程度以及数形结合的思维能力,属于基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
“点M在曲线y2=4x上”是“点M的坐标满足方程2
+y=0“的( )
| x |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |